
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
分析 由题意知[xf(x)]′=$\frac{lnx}{x}$,从而由积分可知xf(x)=$\frac{1}{2}$(lnx)2+c,从而解得f(x)的解析式,从而再求导判断函数的单调性即可判断函数的极值.
解答 解:∵x2f′(x)+xf(x)=lnx,
∴xf′(x)+f(x)=$\frac{lnx}{x}$,
∴[xf(x)]′=$\frac{lnx}{x}$,
∴xf(x)=$\frac{1}{2}$(lnx)2+c,
又∵f(e)=$\frac{1}{e}$,
∴e•$\frac{1}{e}$=$\frac{1}{2}$+c,
故c=$\frac{1}{2}$,
∴f(x)=$\frac{l{n}^{2}x}{2x}$+$\frac{1}{2x}$,
∴f′(x)=$\frac{2lnx×\frac{1}{x}×x-(l{n}^{2}x+1)}{2{x}^{2}}$=$\frac{-(lnx-1)^{2}}{2{x}^{2}}$≤0,
∴f(x)在区间(0,+∞)上是减函数,
∴既无极大值又无极小值.
故选D.
点评 本题考查导数的综合应用,考查了导数的综合应用及积分的应用,考查转化思想,属于中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | -3或3 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
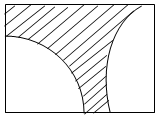 已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.
已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{3}$,2) | B. | [$\frac{3}{4}$,2] | C. | ($\frac{3}{4}$,2) | D. | (-$∞,\frac{3}{4}$)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上)
如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上) 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
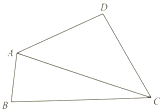 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com