
 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��M��N�ֱ����߶�A1C1��BD�ϵĶ��㣬�������ж���ȷ���Ǣ٢ۢܢݣ�������Ϊ��ȷ����Ŷ����ϣ�
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��M��N�ֱ����߶�A1C1��BD�ϵĶ��㣬�������ж���ȷ���Ǣ٢ۢܢݣ�������Ϊ��ȷ����Ŷ����ϣ� ���� ��M��N�ֱ����߶�A1C1��BD�ϵ��е�ʱ��������ֱ�ߵľ��룬�����жϢ٣�
��M��C1�غϣ�N��B�غϣ��������߶����������жϢڣ�
��M��N�ֱ����߶�A1C1��BD�ϵ��е�ʱ��MNƽ�����������⣬������ƽ�е��ж������������жϢۣ�
������Խ��ߣ�BC1��A1D��A1B��C1D���֣������жϢܣ�
����M��A1C1�ϣ�A1C1ƽ���ڵ���ABCD����M������ľ���Ϊ��ֵ1�������������ʽ�����жϢݣ�
��� 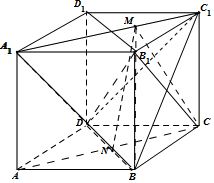 �⣺���ڢ٣�M��N�ֱ����߶�A1C1��BD�ϵĶ��㣬��M��N�ֱ����߶�A1C1��BD�ϵ��е�ʱ��MN��BD��MN��A1C1����MNΪ
�⣺���ڢ٣�M��N�ֱ����߶�A1C1��BD�ϵĶ��㣬��M��N�ֱ����߶�A1C1��BD�ϵ��е�ʱ��MN��BD��MN��A1C1����MNΪ
����ֱ��A1C1��BD�Ĺ����߶Σ������߶�MN����Сֵ������СֵΪ1���ʢٶԣ�
���ڢڣ���M��C1�غϣ�N��B�غϣ�����BC1��B1C��
��BC1��B1C��CD��ƽ��BCC1B1���������߶����ɵ�
B1D��BC1���ʢڴ���
���ڢۣ�����һ��λ�ã���M��N�ֱ����߶�A1C1��BD�ϵ��е�ʱ��MNƽ�����������⣬������ƽ�е��ж�������
�ɵ�ʹMN���ڵ�ֱ�����ĸ����涼ƽ�У��ʢ۶ԣ�
���ڢܣ�$|{MN}|=\sqrt{2}$�����ֻ������Խ��ߣ�BC1��A1D��A1B��C1D���֣��ʢܶԣ�
���ڢݣ�M��N��B��C�ĵ��ܹ�������������M��A1C1�ϣ�
A1C1ƽ���ڵ���ABCD����M������ľ���Ϊ��ֵ1��
�����������ֻ���N��λ���йأ���M�أ��ʢݶԣ�
�ʴ�Ϊ���٢ۢܢݣ�
���� ���⿼��ռ����ߡ������λ�ù�ϵ�;��뼰���������������������������Լ�ת��˼�롢���ν�ϵ�˼�뷽���������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �м���ֵ����Сֵ | B�� | �м�Сֵ������ֵ | ||
| C�� | ���м���ֵ���м�Сֵ | D�� | ������ֵҲ��Сֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
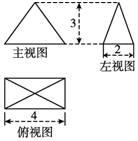
| A�� | 8 | B�� | 8+4$\sqrt{10}$ | C�� | 2$\sqrt{10}$+$\sqrt{13}$ | D�� | 4$\sqrt{10}$+2$\sqrt{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 100 | B�� | 900 | C�� | 999 | D�� | 1000 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{1}{2}$��3�� | B�� | ��-�ޣ�$\frac{1}{2}$]�ȣ�3��+�ޣ� | C�� | [$\frac{1}{3}$��2] | D�� | ��-�ޣ�$\frac{1}{3}$]��[2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
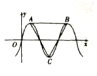 ����$f��x��=3\sqrt{3}sin��x��{�أ�0}��$�IJ���ͼ����ͼ��ʾ����A��B��ͼ�����ߵ㣬��C��ͼ�����͵㣬�ҡ�ABC���������Σ���f��1��+f��2��+f��3����ֵΪ��������
����$f��x��=3\sqrt{3}sin��x��{�أ�0}��$�IJ���ͼ����ͼ��ʾ����A��B��ͼ�����ߵ㣬��C��ͼ�����͵㣬�ҡ�ABC���������Σ���f��1��+f��2��+f��3����ֵΪ��������| A�� | $\frac{9}{2}$ | B�� | $\frac{{9\sqrt{3}}}{2}$ | C�� | $9\sqrt{3}+1$ | D�� | $\frac{{9��{\sqrt{3}+1}��}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com