
| A. | [$\frac{1}{2}$,3) | B. | (-∞,$\frac{1}{2}$]∪(3,+∞) | C. | [$\frac{1}{3}$,2] | D. | (-∞,$\frac{1}{3}$]∪[2,+∞) |
分析 根据函数性质推导f(x)在[-4,-2)上的解析式,计算f(x)在[-4,-2)上的最小值,得出关于t的不等式,从而得出t的范围.
解答 解:∵f(x+2)=$\sqrt{3}$f(x),∴f(x+4)=$\sqrt{3}$f(x+2)=3f(x),
若x∈[-4,-2),则x+4∈[0,2),
∴f(x)=$\left\{\begin{array}{l}{\frac{1}{3}[2(x+4)^{2}-2(x+4)],x∈[-4,-3)}\\{-\frac{2}{3}•(\frac{1}{3})^{|x+\frac{8}{3}|},x∈[-3,-2)}\end{array}\right.$,即f(x)=$\left\{\begin{array}{l}{\frac{2}{3}(x+\frac{7}{2})^{2}-\frac{1}{6},x∈[-4,-3)}\\{-\frac{2}{3}•(\frac{1}{3})^{|x+\frac{8}{3}|},x∈[-3,-2)}\end{array}\right.$,
∴f(x)在[-4,-3)上的最小值为f(-$\frac{7}{2}$)=-$\frac{1}{6}$,
f(x)在[-3,-2)上的最小值为f(-$\frac{8}{3}$)=-$\frac{2}{3}$,
∴f(x)在[-4,-2)上的最小值为-$\frac{2}{3}$,
∵-$\frac{2}{3}$≥t2-$\frac{7}{3}$t,解得$\frac{1}{3}≤t≤2$.
故选C.
点评 本题考查了分段函数的最值计算,函数恒成立问题,属于中档题.


科目:高中数学 来源: 题型:填空题
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上)
如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上) 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{1}{2π}$ | D. | $\frac{π-2}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
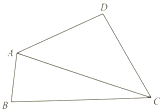 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 30 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com