
分析 (1)设圆C的标准方程为(x-a)2+y2=r2,根据切线的性质列方程组求出a,r即可得出圆C的标准方程;
(2)设直线m的方程y=kx,代入圆的方程化简,利用根与系数的关系得出P,Q的坐标关系,利用距离公式和|PN|2+|QN|2=24列方程解出k.
解答 解:(1)设圆C的标准方程为(x-a)2+y2=r2,
则$\left\{\begin{array}{l}{\frac{|4a-6|}{5}=r}\\{\frac{\frac{6}{5}}{\frac{3}{5}-a}=\frac{3}{4}}\end{array}\right.$,解得a=-1,r=2,
∴圆C的标准方程为:(x+1)2+y2=4.
(2)设直线m的方程为y=kx,(k>0),
代入圆C的方程得(x+1)2+k2x2-4=0,即(1+k2)x2+2x-3=0,
∴x1+x2=$\frac{-2}{1+{k}^{2}}$,y1+y2=k(x1+x2)=$\frac{-2k}{1+{k}^{2}}$,
∴|PN|2=(x1-2)2+(y1-1)2=x12+y12-4x1-2y1+5=3-2x1-4x1-2y1+5=-6x1-2y1+8,
|QN|2=(x2-2)2+(y2-1)2=x22+y22-4x2-2y2+5=3-2x2-4x2-2y2+5=-6x2-2y2+8,
∴|PN|2+|QN|2=-6(x1+x2)-2(y1+y2)+16=$\frac{12}{1+{k}^{2}}$+$\frac{4k}{1+{k}^{2}}$+16=24,
解得k=1或k=-$\frac{1}{2}$(舍).
∴直线m的方程为:y=x.
点评 本题考查了圆的标准方程,直线与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 都是增函数 | B. | f(x)为减函数,g(x)为增函数 | ||
| C. | 都是减函数 | D. | f(x)为增函数,g(x)为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | |||
| 学习积极性一般 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
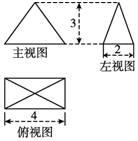
| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 2$\sqrt{10}$+$\sqrt{13}$ | D. | 4$\sqrt{10}$+2$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com