
分析 首先化简三角函数式,然后利用三角函数的图象变换确定平移长度.
解答 解:函数$f(x)=2\sqrt{3}sin({x+\frac{π}{4}})cos({x+\frac{π}{4}})-sin({2x+3π})$
=$\sqrt{3}$sin(2x+$\frac{π}{2}$)+sin2x
=$\sqrt{3}$cos2x+sin2x
=2sin(2x+$\frac{π}{3}$),
所以要得到函数$y=2sin({2x-\frac{π}{3}})$的图象,只需把函数向右平移$\frac{π}{3}$个单位长度;
故答案为:向右平移$\frac{π}{3}$个单位长度.
点评 本题考查了三角函数式的化简与函数图象的平移变换;正确化简三角函数式是关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (0,1] | B. | (-2,-1)∪[0,1] | C. | [-1,0]∪(1,2) | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
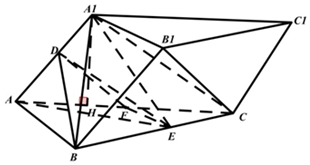 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com