
分析 (1)由题意,利用列举法确定基本事件事件(a,b),从而求事件A的概率P(A);
(2)在区间[0,2]内任取两个实数x,y,全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B构成的区域B={(x,y)|x2+y2≥4,(x,y)∈Ω},求出相应的面积,利用几何概型可求得结论.
解答 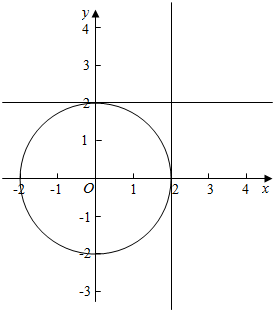 解:(1)由题意,基本事件有如下12个
解:(1)由题意,基本事件有如下12个
(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)
(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),
事件A包含的基本事件为如下4个:
(2,4),(3,4),(4,2),(4,3),
∴P(A)=$\frac{4}{12}=\frac{1}{3}$;
(2)在区间[0,2]内任取两个实数x,y,全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2≥4,(x,y)∈Ω},
所以P(B)=1-$\frac{π}{4}$.
点评 本题考查等可能事件的概率,考查几何概型,解题的关键是确定其测度.


科目:高中数学 来源: 题型:解答题
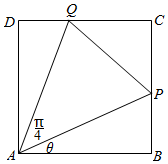 如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.
如图,某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区,在其余土地种植绿化,住宅区形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知,∠PAQ=$\frac{π}{4}$,设∠PAB=θ,记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$,若L越大,则住宅区绿化越好.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )
如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为( )| A. | 0.2 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com