
【题目】如图,正方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
(Ⅱ)求证:平面![]() ∥平面
∥平面![]() ;
;
(Ⅲ)画出平面![]() 与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
(Ⅰ)要证![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,只需证明
四点共面,只需证明![]() ∥
∥![]() ;
;
(Ⅱ)只需证明![]() ∥平面
∥平面![]() ,
,![]() ∥平面
∥平面![]() 即可;
即可;
(Ⅲ)因为![]() ∥平面
∥平面![]() ,
,![]() 平面
平面![]() ,设平面
,设平面![]() 平面
平面![]() ,由线面平行的性质定理知
,由线面平行的性质定理知![]() ∥
∥![]() ,过
,过![]() 作
作![]() 的平行线即可.
的平行线即可.
(Ⅰ)因为![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ∥
∥![]() ,
,
又四边形![]() 是矩形,所以
是矩形,所以![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
(Ⅱ)由已知,![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
同理![]() ∥
∥![]() ∥
∥![]() ,且
,且![]()
![]()
![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
又![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() .
.
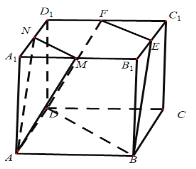
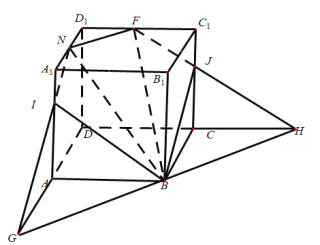
(Ⅲ)∴过![]() 作
作![]() 的平行线交
的平行线交![]() 分别于
分别于![]() ,连接
,连接![]() 分别交
分别交![]() 于
于![]() ,连接
,连接![]() ,如图,
,如图,
理由如下:因为![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() ∥平面
∥平面![]() ,
,![]() 平面
平面![]() ,设平面
,设平面![]() 平面
平面![]() ,
,
由线面平行的性质定理知![]() ∥
∥![]() ,所以过
,所以过![]() 作
作![]() 的平行线交
的平行线交![]() 分别于
分别于![]() ,连
,连
接![]() 分别交
分别交![]() 于
于![]() ,连接
,连接![]() ,即可得到平面
,即可得到平面![]() 与正方体侧面的交
与正方体侧面的交
线.


科目:高中数学 来源: 题型:
【题目】大庆实验中学在高二年级举办线上数学知识竞赛,在已报名的400名学生中,根据文理学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
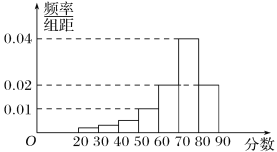
(1)估算一下本次参加考试的同学成绩的中位数和众数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半理科生的分数不小于70,且样本中分数不小于70的文理科生人数相等.试估计总体中理科生和文科生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
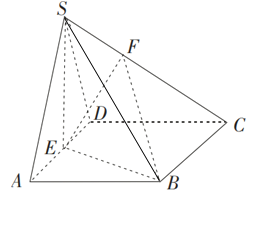
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当∠AOB为锐角时,求k的取值范围;
,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点。
是否过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
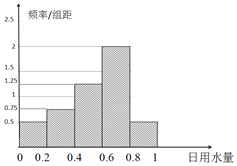
【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
频数(天) | 2 | 5 | 7 | 3 | 3 |
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:![]() xiyi=65,
xiyi=65,![]() 612
612
参考公式:回归方程![]() x
x![]() 中斜率和截距的公式分别为:
中斜率和截距的公式分别为:
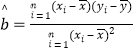 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com