
分析 (1)设动点坐标M(x,y)利用两点之间的距离公式建立关系,可得M的轨迹方程.
(2)解法一:由(1)可知轨迹C是圆,利用圆心到直线的距离大于半径,可求k的取值范围.
解法二,直线y=kx-5与轨迹C联立方程组,消去x(或y),利用判别式△<0,没有交点k的取值范围.
解答 解:(1)由题意:设动点坐标M(x,y),则$\sqrt{(x-8)^{2}+{y}^{2}}=\sqrt{(x-2)^{2}+{y}^{2}}$,
整理得:x2+y2=16.
即动点M的轨迹C的方程为:x2+y2=16.
(2)解法一:由(1)可知轨迹C是圆,圆心(0,0),半径r=4,
由圆心到直线的距离d$\frac{|5|}{\sqrt{{k}^{2}+1}}>4$,
解得:$-\frac{3}{4}<k<\frac{3}{4}$.
解法二:直线y=kx-5与轨迹C联立方程组,即:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=16}\\{y=kx-5}\end{array}\right.$,消去y,并化简可得:(1+k2)x2-10kx+9=0,
∵直线y=kx-5与轨迹C没有交点,
所以:△=b2-4ac=100k2-36(1+k2)<0,
即16k2-9<0,
解得:$-\frac{3}{4}<k<\frac{3}{4}$.
故得k的取值范围是($-\frac{3}{4}$,$\frac{3}{4}$).
点评 本题主要考查轨迹方程的求法和直线和圆的位置关系的判断,根据直线和圆没有交点即判别式小于0(或者利用圆心到直线的距离大于半径)求解是关键.属于基础题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
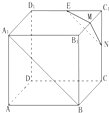 如图,在正方体ABCD-A1B1C1D1中,棱长为2,M、N、E分别为B1C1、C1C、D1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,棱长为2,M、N、E分别为B1C1、C1C、D1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 96种 | B. | 78种 | C. | 72种 | D. | 36种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 126 | B. | 63 | C. | 64 | D. | 127 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p1 | B. | p1∧p2 | C. | p2∧p3 | D. | p1∧(¬p3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
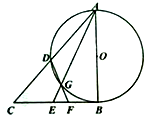 如图,AB是⊙O的直径,CB与⊙O相切与点B,E为线段CB上一点,
如图,AB是⊙O的直径,CB与⊙O相切与点B,E为线段CB上一点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com