
【题目】如图,三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 面
面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
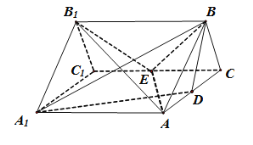
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,从而平面
,从而平面![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() ,
,![]() ,再求出
,再求出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)本问方法较多,可用割补法,转换顶点法,构造法等,其中割补法较为方便,将![]() 转化为
转化为![]() ,即可求解.
,即可求解.
解:(1)∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵三棱柱![]() 中
中![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵在正方形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
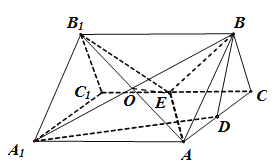
(2)解法一(割补法):
![]()
![]()
![]() .
.
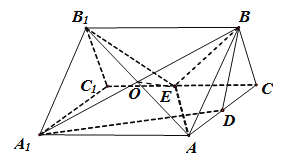
解法二(利用平行顶点轮换):
∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
解法三(利用对称顶点轮换):
连结![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
∴![]()
![]() .
.
解法四(构造法):
连结![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,再连结
的中点,再连结![]() .
.
由题意知在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,
,
∴![]() 面
面![]() ,
,
∴![]()
![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】秉承提升学生核心素养的理念,学校开设以提升学生跨文化素养为核心的多元文化融合课程.选某艺术课程的学生唱歌、跳舞至少会一项,已知会唱歌的有![]() 人,会跳舞的有
人,会跳舞的有![]() 人,现从中选
人,现从中选![]() 人,设
人,设![]() 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且![]()
(1)求选该艺术课程的学生人数;
(2)写出![]() 的概率分布列并计算
的概率分布列并计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
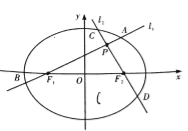
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有多少种
A.60B.90C.120D.150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水污染现状与工业废水排放密切相关,某工厂深人贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有4个标准水量的A级水池,分别取样、检测,多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有样本不达标,则混合样本的化验结果必不达标,若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放
现有以下四种方案:
方案一:逐个化验;
方案二:平均分成两组化验;方案三;三个样本混在一起化验,剩下的一个单独化验;
方案四:四个样本混在一起化验.
化验次数的期望值越小,则方案越"优".
(1)若![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(2)①若![]() ,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0 (n∈N ),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设![]() ,数列{bn}的前n项和为Sn,当
,数列{bn}的前n项和为Sn,当![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义一:对于一个函数![]() ,若存在两条距离为d的直线
,若存在两条距离为d的直线![]() 和
和![]() ,使得在
,使得在![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在D内有一个宽度为d的通道.定义二:若一个函数
在D内有一个宽度为d的通道.定义二:若一个函数![]() ,对于任意给定的正数
,对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.下列函数:①
在正无穷处有永恒通道.下列函数:①![]() ;②
;②![]() ;③
;③![]() .其中在正无穷处有永恒通道的函数的个数为( )
.其中在正无穷处有永恒通道的函数的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成,它的轴截面如图所示,已知半球的直径是![]() ,圆柱筒高
,圆柱筒高![]() ,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆
,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 及
及![]() 焊接而成,其中
焊接而成,其中![]() ,
,![]() 分别是圆柱上下底面的圆心,
分别是圆柱上下底面的圆心,![]() ,
,![]() ,
,![]() ,
,![]() 均在“浮球”的内壁上,AC,BD通过“浮球”中心
均在“浮球”的内壁上,AC,BD通过“浮球”中心![]() ,且
,且![]() 、
、![]() 均与圆柱的底面垂直.
均与圆柱的底面垂直.
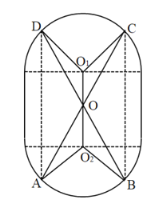
(1)设![]() 与圆柱底面所成的角为
与圆柱底面所成的角为![]() ,试用
,试用![]() 表示出防压卡中四边形
表示出防压卡中四边形![]() 的面积
的面积![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)研究表明,四边形![]() 的面积越大,“浮球”防压性越强,求四边形
的面积越大,“浮球”防压性越强,求四边形![]() 面积取最大值时,点
面积取最大值时,点![]() 到圆柱上底面的距离
到圆柱上底面的距离![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com