
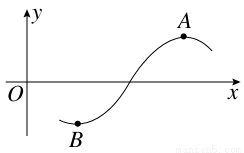
函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A,B分别为该部分图象的最高点与最低点,且这两点间的距离为4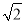 ,则函数f(x)图象的一条对称轴的方程为( )
,则函数f(x)图象的一条对称轴的方程为( )
A.x=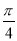 B.x=
B.x=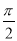 C.x=4 D.x=2
C.x=4 D.x=2
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
已知△ABC的三边长为a,b,c,且面积S△ABC= (b2+c2-a2),则A=( )
(b2+c2-a2),则A=( )
A.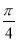 B.
B.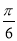 C.
C.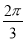 D.
D.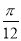
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:选择题
已知 =5,则sin2α-sinαcosα的值是( )
=5,则sin2α-sinαcosα的值是( )
A. B.-
B.-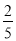 C.-2 D.2
C.-2 D.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知函数f(x)=2cosxsin(x+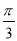 )-
)- sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=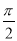 对称,求m的最小正值.
对称,求m的最小正值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
设函数y=sin(ωx+φ)(ω>0,φ∈(- ,
,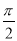 ))的最小正周期为π,且其图象关于直线x=
))的最小正周期为π,且其图象关于直线x= 对称,则在下面四个结论中:①图象关于点(
对称,则在下面四个结论中:①图象关于点(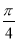 ,0)对称;②图象关于点(
,0)对称;②图象关于点( ,0)对称;③在[0,
,0)对称;③在[0, ]上是增函数;④在[-
]上是增函数;④在[-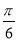 ,0]上是增函数,所有正确结论的编号为________.
,0]上是增函数,所有正确结论的编号为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
牛奶保鲜时间因储藏温度的不同而不同,假定保鲜时间与储藏温度的关系为指数型函数y=kax,若牛奶在0℃的冰箱中,保鲜时间约为100 h,在5℃的冰箱中,保鲜时间约为80 h,那么在10℃时保鲜时间约为( )
A.49 h B.56 h C.64 h D.72 h
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
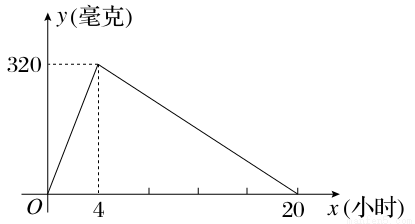
A.上午10:00 B.中午12:00
C.下午4:00 D.下午6:00
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:选择题
直线y=x与函数f(x)= 的图象恰有三个公共点,则实数m的取值范围是( )
的图象恰有三个公共点,则实数m的取值范围是( )
A.[-1,2) B.[-1,2] C.[2,+∞) D.(-∞,-1]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:填空题
已知函数f(x)=2|2x-m|(m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com