
已知函数f(x)=2cosxsin(x+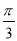 )-
)- sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=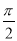 对称,求m的最小正值.
对称,求m的最小正值.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:解答题
如图所示,在四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.

(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:填空题
已知函数f(x)=2sin2(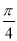 +x)-
+x)-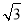 cos2x-1,x∈[
cos2x-1,x∈[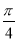 ,
,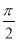 ],则f(x)的最小值为________.
],则f(x)的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:

①最小正周期为π;
②将f(x)的图象向左平移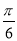 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④f(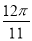 )<f(
)<f(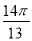 );
);
⑤f(x)=-f( -x).
-x).
其中正确的是( )
A.①②③ B.②③④ C.①④⑤ D.②③⑤
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
要得到函数y=3sin(2x+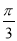 )的图象,只需要将函数y=3cos2x的图象( )
)的图象,只需要将函数y=3cos2x的图象( )
A.向右平移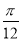 个单位 B.向左平移
个单位 B.向左平移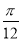 个单位
个单位
C.向右平移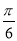 个单位 D.向左平移
个单位 D.向左平移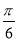 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
设函数f(x)=sin(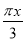 -
-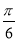 )-2cos2
)-2cos2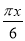 .
.
(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:选择题
函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A,B分别为该部分图象的最高点与最低点,且这两点间的距离为4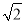 ,则函数f(x)图象的一条对称轴的方程为( )
,则函数f(x)图象的一条对称轴的方程为( )
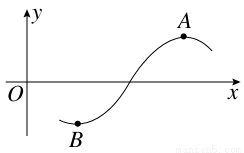
A.x=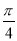 B.x=
B.x=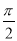 C.x=4 D.x=2
C.x=4 D.x=2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
某种商品进价为每件100元,按进价增加25%出售,后因库存积压降价,按九折出售,每件还获利( )
A.25元 B.20.5元 C.15元 D.12.5元
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:填空题
已知函数f(x)=ln(1-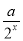 )的定义域是(1,+∞),则实数a的值为________.
)的定义域是(1,+∞),则实数a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com