
设函数f(x)=sin(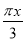 -
-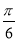 )-2cos2
)-2cos2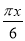 .
.
(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
有一长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长的长度(单位:m)是( )
A.5 B.10 C.10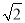 D.10
D.10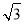
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:解答题
已知函数f(x)=- sin(2x+
sin(2x+ )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:填空题
若将函数y=sin(ωx+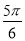 )(ω>0)的图象向右平移
)(ω>0)的图象向右平移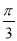 个单位长度后,与函数y=sin(ωx+
个单位长度后,与函数y=sin(ωx+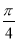 )的图象重合,则ω的最小值为________.
)的图象重合,则ω的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知函数f(x)=2cosxsin(x+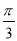 )-
)- sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=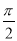 对称,求m的最小正值.
对称,求m的最小正值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:选择题
若函数f(x)=2sin(2x+φ)(|φ|<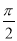 )与g(x)=cos(ωx-
)与g(x)=cos(ωx- )(ω>0)的图象具有相同的对称中心,则φ=( )
)(ω>0)的图象具有相同的对称中心,则φ=( )
A.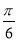 B.
B. C.-
C.- D.-
D.-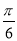
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
牛奶保鲜时间因储藏温度的不同而不同,假定保鲜时间与储藏温度的关系为指数型函数y=kax,若牛奶在0℃的冰箱中,保鲜时间约为100 h,在5℃的冰箱中,保鲜时间约为80 h,那么在10℃时保鲜时间约为( )
A.49 h B.56 h C.64 h D.72 h
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:解答题
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:选择题
函数y=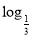 (-x2+6x)的值域( )
(-x2+6x)的值域( )
A.(0,6) B.(-∞,-2] C.[-2,0) D.[-2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com