

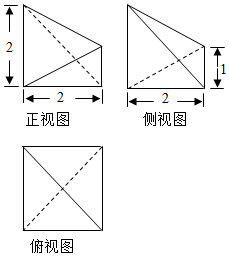
Ζ÷Έω Θ®1Θ©ΗυΨίΧβ“βΩ…÷Σ…η≥ω÷±œΏΖΫ≥ΧΘ§”…«–œΏ–±¬ ΒΡΕ®“εΦ¥Ω…±μ Ψ≥ω÷±œΏBCΒΡ–±¬ ΘΜ
Θ®2Θ©«σΒΟ«–œΏΒΡ–±¬ Θ§Ω…ΒΟDΒΡΉχ±ξΘ§«σΒΟ÷±œΏBCΒΡΖΫ≥ΧΘ§‘Υ”Ο÷–ΒψΉχ±ξΙΪ ΫΩ…ΒΟAΙΊ”ΎDΒΡΕ‘≥ΤΒψ‘Ύ÷±œΏBC…œΘ§«σΒΟDΈΣAEΒΡ÷–ΒψΘ§ΗυΨίMNΈΣ»ΐΫ«–ΈABCΒΡ÷–ΈΜœΏΘ§«“EΈΣBCΒΡ÷–ΒψΘ§DΈΣMNΒΡ÷–ΒψΘ§«σΒΟ»ΐΫ«–ΈABCΒΡΟφΜΐΘ§‘Ό”…»ΐΫ«–ΈΒΡΟφΜΐ÷°±»”κΕ‘”Π±ΏΒΡ±»ΒΡΙΊœΒΘ§Ω…ΒΟ”…≈ΉΈοœΏΆβΉς≥ωΒΡΓΑ«–œΏ»ΐΫ«–ΈΓ±ΒΡΟφΜΐΙΙ≥…“‘$\frac{1}{4}$SΈΣ ΉœνΘ§$\frac{1}{4}$ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§‘Υ”ΟΈό«νΒίΥθΒ»±» ΐΝ–ΒΡ«σΚΆΙΪ ΫΘ§Ω…ΒΟΥυ”–ΟφΜΐΚΆΘ§Φ¥Ω…ΒΟΒΫΥυ«σΟφΜΐTΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…η«–œΏΖΫ≥ΧΈΣy-y0=$\frac{p}{{y}_{0}}$Θ®x-x0Θ©Θ§
kBC=$\frac{{y}_{B}-{y}_{C}}{{x}_{B}-{x}_{C}}$=$\frac{2p}{s+t}$Θ§
Θ®2Θ©…ηDΘ®ΠΧΘ§vΘ©Θ§‘ρMNΓΈBCΘ§
Γύ$\frac{p}{v}$=$\frac{2p}{s+t}$Θ§Θ®sΘ§tΈΣBΘ§CΒΡΉίΉχ±ξΘ©Θ§
v=$\frac{s+t}{2}$DΘ®$\frac{Θ®s+tΘ©^{2}}{8p}$Θ§$\frac{s+t}{2}$Θ©Θ§
…ηAΘ®aΘ§bΘ©άϊ”Ο«–œΏΖΫ≥ΧΒΟΘΚ
$\left\{\begin{array}{l}{b-t=\frac{p}{t}Θ®a-\frac{{t}^{2}}{2p}Θ©}\\{b-s=\frac{p}{s}Θ®a-\frac{{s}^{2}}{2p}Θ©}\end{array}\right.$Φ¥$\left\{\begin{array}{l}{bt=ap+\frac{{t}^{2}}{2}}\\{bt=ap-\frac{{s}^{2}}{2}}\end{array}\right.$Θ§ΝΫ ΫœύΦθΒΟΘΚ
b=$\frac{t+s}{2}$Θ§a=$\frac{st}{2p}$Θ§AΘ®$\frac{st}{2p}$Θ§$\frac{t+s}{2}$Θ©Θ§
”…«ΑΟφΦΤΥψΩ…÷ΣΘΚADΤΫ––”ΎΚα÷αΘ§Ω…ΒΟyE=$\frac{t+s}{2}$Θ§
BCΘΚy-t=$\frac{2p}{s+t}$Θ®x-$\frac{{t}^{2}}{2p}$Θ©Θ§ΫΪyE=$\frac{t+s}{2}$Θ§¥ζ»κxE=$\frac{{s}^{2}+{t}^{2}}{4p}$Θ§
”…xA+xE=$\frac{st}{2p}$+$\frac{{s}^{2}+{t}^{2}}{4p}$=$\frac{Θ®s+tΘ©^{2}}{4p}$=2xDΘ§
Υυ“‘DΈΣAEΒΡ÷–ΒψΘΜ
…ηΘΚSΓςAMN=RΘ§”……œΩ…÷ΣR=$\frac{1}{4}$SΓςABC=$\frac{S}{4}$Θ§
”…MΘ§N»ΖΕ®ΒΡ»ΖΕ®ΒΡ«–œΏ»ΐΫ«–ΈΒΡΟφΜΐΈΣ$\frac{1}{4}$ΓΝ$\frac{R}{2}$=$\frac{R}{8}$Θ§
Κσ“ΜΗω«–œΏ»ΐΫ«–ΈΒΡΟφΜΐ ««Α“Μ«–œΏ»ΐΫ«–ΈΟφΜΐΒΡ$\frac{1}{8}$Θ§
”…¥ΥΦΧ–χœ¬»ΞΩ…ΒΟΥψ ΫΘΚ
SΓςABC=S=T+R+2$\frac{R}{8}$+4$\frac{R}{64}$+8$\frac{R}{512}$+Γ≠+Θ§
=T+R+$\frac{R}{4}$+$\frac{R}{16}$+$\frac{R}{64}$+Γ≠Θ§
ΓύT=S-$\frac{R}{1-\frac{1}{4}}$=S-$\frac{4}{3}$R=$\frac{2}{3}$SΘ°
ΒψΤά ±ΨΧβΩΦ≤ι÷±œΏΚΆ≈ΉΈοœΏΒΡΈΜ÷ΟΙΊœΒΘ§÷ς“Σ «œύ«–ΒΡΧθΦΰΘ§ΩΦ≤ι÷±œΏΒΡ–±¬ ΚΆΖΫ≥ΧΒΡ‘Υ”ΟΘ§Ά§ ±ΩΦ≤ι»ΐΫ«–ΈΒΡΟφΜΐΒΡ«σΖ®Θ§ΉΔ“β‘Υ”Ο»ΐΫ«–ΈΟφΜΐ÷°±»”κΕ‘”Π±ΏΒΡ±»ΒΡΙΊœΒΘ§ΩΦ≤ι‘ΥΥψΡήΝΠΘ§ΨΏ”–“ΜΕ®ΒΡΡ―Ε»Θ§ τ”Ύ÷–ΒΒΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ÷±Ϋ«»ΐΫ«–Έ | BΘ° | Β»±Ώ»ΐΫ«–Έ | CΘ° | ΕέΫ«»ΐΫ«–Έ | DΘ° | Β»―ϋ÷±Ϋ«»ΐΫ«–Έ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δ“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| x | 4 | 5 | 6 |
| y | 8 | 6 | 7 |
| AΘ° | 1 | BΘ° | $\frac{3}{2}$ | CΘ° | $\frac{4}{5}$ | DΘ° | $\frac{5}{6}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2 | BΘ° | $\sqrt{2}$ | CΘ° | 4 | DΘ° | 2$\sqrt{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2 | BΘ° | $\frac{4\sqrt{2}}{3}$ | CΘ° | $\frac{4\sqrt{3}}{3}$ | DΘ° | 3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
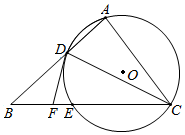 »γΆΦΘ§‘ΎΓςABC÷–Θ§CD «ΓœACBΒΡΫ«ΤΫΖ÷œΏΘ§ΓςACDΒΡΆβΫ”‘≤Γ―OΫΜBC”ΎΒψEΘ§DF «Γ―OΒΡ«–œΏΫΜBC”ΎΒψFΘ§«“EC=3EF=3Θ°
»γΆΦΘ§‘ΎΓςABC÷–Θ§CD «ΓœACBΒΡΫ«ΤΫΖ÷œΏΘ§ΓςACDΒΡΆβΫ”‘≤Γ―OΫΜBC”ΎΒψEΘ§DF «Γ―OΒΡ«–œΏΫΜBC”ΎΒψFΘ§«“EC=3EF=3Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com