
【题目】设函数![]() .
.
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,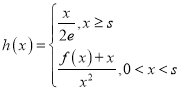 ,若对任意实数
,若对任意实数![]() ,总存在正实数
,总存在正实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
【答案】(1)![]() =
=![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)讨论![]() ,
,![]() 和
和![]() 三种情况,分别计算得到答案.
三种情况,分别计算得到答案.
(2)求导得到![]() ,讨论
,讨论![]() ,
,![]() ,
,![]() 三种情况,分别计算得到答案.
三种情况,分别计算得到答案.
(3)![]() 在
在![]() 上是增函数,其值域为
上是增函数,其值域为![]() ,若
,若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数,值域为
上是增函数,值域为![]() ,记
,记![]() ,则
,则![]()
根据![]() 得到答案.
得到答案.
(1)若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,
,![]() ,不合题意;
,不合题意;
若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,
,![]() ,不合题意;
,不合题意;
若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,满足题意,因此
,满足题意,因此![]() =
=![]() .
.
(2)![]() ,
,![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此![]() 点,在
点,在![]()
(i)当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 内至多有一个极值点.
内至多有一个极值点.
(ii)当![]() 时,由于
时,由于![]() ,所以
,所以![]() ,
,
而![]() ,
,![]() ,
,![]() ,
,
因此![]() 在
在![]() 上无零点,在
上无零点,在![]() 上有且仅有一个零点,
上有且仅有一个零点,
从而![]() 上有且仅有一零点,
上有且仅有一零点,![]() 在
在![]() 内有且仅有一个极值点.
内有且仅有一个极值点.
(iii)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
因此![]() 在
在![]() 上有且仅有一个零点,
上有且仅有一个零点,
从而![]() 在上有且仅有两个零点,
在上有且仅有两个零点,![]() 在
在![]() 内有且仅有两个极值点.
内有且仅有两个极值点.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
(3)因为对任意实数,总存在实数![]() ,使得
,使得![]() 成立,
成立,
所以函数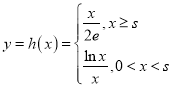 的值域为
的值域为![]() .
.
![]() 在
在![]() 上是增函数,其值域为
上是增函数,其值域为![]() ,
,
对于函数![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上为单调减函数,
上为单调减函数,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上为单调增函数.
上为单调增函数.
若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,其值域为
上是减函数,其值域为![]() ,又
,又![]() ,不符合题意,舍去;
,不符合题意,舍去;
若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数,值域为
上是增函数,值域为![]() ,
,
由题意得![]() ,即
,即![]() ①
①
记![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调减函数.
上为单调减函数.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调增函数.所以,当
上为单调增函数.所以,当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
从而![]() 恒成立(当且仅当
恒成立(当且仅当![]() 时,
时,![]() ②
②
由①②得,![]() ,所以
,所以![]() .
.
综上所述,正实数的取值集合为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1,2. 第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2; 那么第10次“H扩展”后得到的数列的所有项的和为( )
A.88572B.88575C.29523D.29526
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为 _____.
查看答案和解析>>
科目:高中数学 来源: 题型:
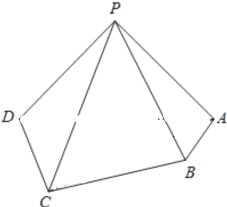
【题目】如图,在四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在, 求
?若存在, 求![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() (
(![]() 、
、![]() 为实常数).
为实常数).
(1)当![]() 时,证明:
时,证明:![]() 不是奇函数;
不是奇函数;
(2)设![]() 是奇函数,求
是奇函数,求![]() 与
与![]() 的值;
的值;
(3)当![]() 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集![]() ,对任何属于
,对任何属于![]() 的
的![]() 、
、![]() ,都有
,都有![]() 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com