
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:填空题
①函数y=cos(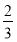 x+
x+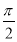 )是奇函数;
)是奇函数;
②存在实数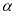 ,使得sin
,使得sin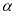 +cos
+cos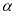 =2;
=2;
③若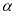 、
、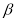 是第一象限角且
是第一象限角且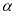 <
<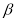 ,则tan
,则tan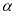 <tan
<tan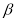 ;
;
④x=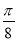 是函数y=sin(2x+
是函数y=sin(2x+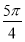 )的一条对称轴方程;
)的一条对称轴方程;
⑤函数y=tan(2x+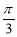 )的图象关于点(
)的图象关于点(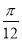 ,0)成中心对称图形.
,0)成中心对称图形.
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程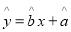 中的
中的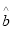 为
为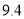 ,据此模型预报广告费用为6万元时销售额为 ( )
,据此模型预报广告费用为6万元时销售额为 ( )
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
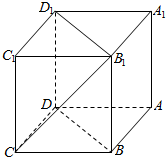 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
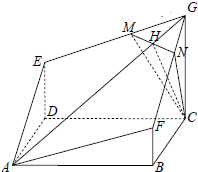 如图是某直四棱柱被平面α所截得的部分,底面ABCD是矩形,侧棱GC、ED、FB都垂直于底面ABCD,GC=3,AB=2$\sqrt{2}$,BC=$\sqrt{5}$.
如图是某直四棱柱被平面α所截得的部分,底面ABCD是矩形,侧棱GC、ED、FB都垂直于底面ABCD,GC=3,AB=2$\sqrt{2}$,BC=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
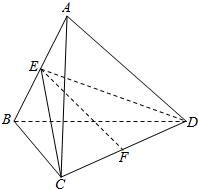 如图,正四面体ABCD的棱长为1.
如图,正四面体ABCD的棱长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com