
已知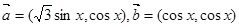 ,
,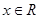 ,函数
,函数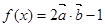 ;
;
(I)求 的最小正周期;
的最小正周期;
(II)求 在区间
在区间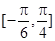 上的最大值和最小值。
上的最大值和最小值。
(I) 的最小正周期为
的最小正周期为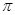 ;
;
(II)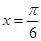 时,函数
时,函数 取得最大值2;
取得最大值2;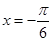 时,函数
时,函数 取得最小值
取得最小值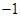 ;
;
解析试题分析:(法一)(I)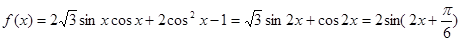 ,
,
函数 的最小正周期为
的最小正周期为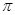 ; 4分
; 4分
(II)因为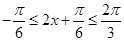 , 5分
, 5分
所以,当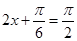 即
即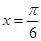 时,函数
时,函数 取得最大值2;
取得最大值2;
当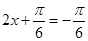 即
即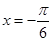 时,函数
时,函数 取得最小值
取得最小值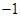 ; 9分
; 9分
(法二)(I) ,
,
函数 的最小正周期为
的最小正周期为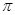 ; 4分
; 4分
(II)因为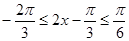 , 5分
, 5分
所以,当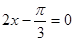 即
即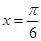 时,函数
时,函数 取得最大值2;
取得最大值2;
当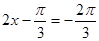 即
即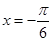 时,函数
时,函数 取得最小值
取得最小值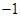 ; 9分
; 9分
考点:本题主要考查平面向量的数量积,三角函数中两角和的正、余弦公式、二倍角公式;三角函数的周期、单调、最值等性质;考查三角函数与平面向量的综合运用能力和化归与转化思想。
点评:典型题,为研究三角函数的图象和性质,往往需要将函数“化一”,这是常考题型。本题首先通过平面向量的坐标运算,计算向量的数量积得到函数F(x)的表达式,并运用“三角公式”进行化简,为进一步解题奠定了基础。


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知向量: ,函数
,函数 ,若
,若 相邻两对称轴间的距离为
相邻两对称轴间的距离为
(Ⅰ)求 的值,并求
的值,并求 的最大值及相应x的集合;
的最大值及相应x的集合;
(Ⅱ)在△ABC中, 分别是A,B,C所对的边,△ABC的面积
分别是A,B,C所对的边,△ABC的面积 ,求边
,求边 的长。
的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com