
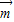 =(2a,b),
=(2a,b),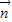 =(a,-3b),且
=(a,-3b),且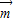 ⊥
⊥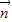 ,(
,(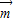 +
+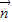 )•(-
)•(-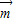 +
+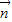 )=14,求a,b,c.
)=14,求a,b,c.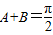 判断出△ABC为直角三角形.
判断出△ABC为直角三角形.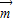 ⊥n,把向量的坐标代入求得2a2-3b2=0,进而根据,(
⊥n,把向量的坐标代入求得2a2-3b2=0,进而根据,(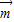 +
+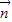 )•(-
)•(-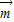 +
+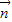 )=14,求得a和b的另一关系式,进而联立方程求得a和b,进而用勾股定理求得c.
)=14,求得a和b的另一关系式,进而联立方程求得a和b,进而用勾股定理求得c. ,2A,2B∈(0,π)
,2A,2B∈(0,π)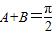 ,故△ABC为直角三角形
,故△ABC为直角三角形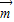 ⊥
⊥ ,所以2a2-3b2=0①
,所以2a2-3b2=0①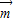 +
+ )•(-
)•(-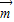 +
+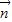 )=
)=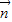 2-
2-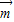 2=14,即8b2-3a2=14②
2=14,即8b2-3a2=14②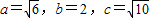


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
| 5π |
| 12 |
| A |
| 2 |
| π |
| 3 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
3
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com