
(本小题满分12分)
已知直三棱柱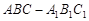 中,
中,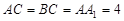 ,
, 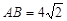 ,若
,若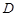 是
是 中点.
中点.
(Ⅰ)求证: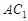 ∥平面
∥平面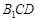 ;
;
(Ⅱ)求异面直线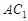 和
和 所成的角.
所成的角.
(1)根据中位线的性质可知,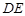 //
//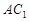 ,那么结合线面平行的判定定理来得到
,那么结合线面平行的判定定理来得到
(2) 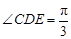
解析试题分析:(Ⅰ)证明:连接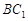 交
交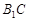 于点
于点 ,连结
,连结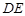 ,
,

 是直三棱柱,
是直三棱柱,
∴三棱柱 的侧面都是矩形,
的侧面都是矩形,
∴点 是
是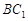 的中点, ………………………2分
的中点, ………………………2分
又
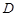 是
是 的中点,
的中点,
∴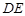 //
//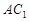 , ………………………4分
, ………………………4分
又∵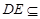 平面
平面 ,
,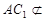 平面
平面
∴ 平面
平面 . ………………………6分
. ………………………6分
(Ⅱ)
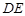 //
//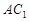 ,
,
∴ 为异面直线
为异面直线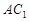 和
和 所成的角或其补角, ………………………7分
所成的角或其补角, ………………………7分
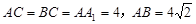 ,
,
∴三角形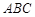 是直角三角形, ………………………8分
是直角三角形, ………………………8分
∴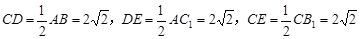 ,
,
∴三角形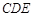 是等边三角形, ………………………11分
是等边三角形, ………………………11分
∴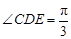 . ………………………12分
. ………………………12分
考点:本试题考查了线面平行和异面直线的所成的角。
点评:解决该试题的关键是能熟练的运用空间中线面平行的判定定理,以及平移法来得到异面直线的所成的角而且平移一般运用中位线法得到,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知△BCD中,∠BCD=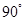 ,BC=CD=1,AB⊥平面BCD,∠ADB=
,BC=CD=1,AB⊥平面BCD,∠ADB=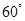 ,E、F分别是AC、AD上的动点,且
,E、F分别是AC、AD上的动点,且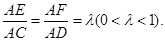
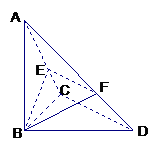
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面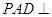 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.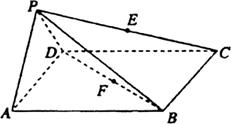
(1)求证: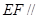 平面PAD;
平面PAD;
(2)求证:平面PDC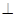 平面PAD;
平面PAD;
(3)求四棱锥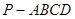 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,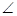 BCD=60
BCD=60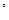 ,E是CD的中点,PA
,E是CD的中点,PA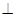 底面ABCD,PA=2.
底面ABCD,PA=2.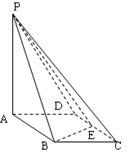
(1)证明:平面PBE 平面PAB;
平面PAB;
(2)求平面PAD和平面PBE所成二面角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)如图,在长方体ABCD-A1B1C1D1中,E, F分别是棱BC,CC1上的点,CF="AB=2CE," AB:AD:AA1=1:2:4.
(Ⅰ)求异面直线EF与A1D所成角的余弦值;
(Ⅱ)证明AF⊥平面A1ED;
(Ⅲ)求二面角A1-ED-F的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com