
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
(1)因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心,因此证明。
(2)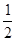 a
a
(3)arctan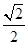 。
。
解析试题分析:(1)由AA1=AD=AB,及∠A1AD=∠A1AB=60° △A1AD、△AA1B都是正三角形,从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心。所以四棱锥A1—ABCD是正四棱锥。
△A1AD、△AA1B都是正三角形,从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心。所以四棱锥A1—ABCD是正四棱锥。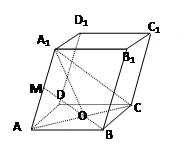
(2)由DB⊥平面AA1O 截面BB1D1D⊥平面AA1O
截面BB1D1D⊥平面AA1O 点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离。取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM=
点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离。取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM=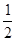 A1C=
A1C=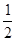 a,∴所求距离为
a,∴所求距离为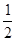 a。
a。
(3)注意到所求二面角的棱是B1B,由M是AA1的中点 MB⊥AA1,B1B∥AA1
MB⊥AA1,B1B∥AA1 MB⊥B1B,又DB⊥AA1,AA1//B1B
MB⊥B1B,又DB⊥AA1,AA1//B1B DB⊥B1B,
DB⊥B1B,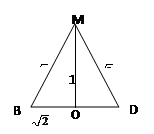
∴∠MBD是所求二面角的平面角。不妨设AB=a=2,则BD=2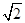 ,MB=MD=
,MB=MD=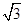 ,
,
∴tanMBD=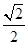 。
。
∴侧面A1ABB1与截面B1BDD1的夹角为arctan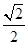 。
。
考点:本试题考查了距离和角的求解运用。
点评:对于立体几何中的角和距离的求解是高考的一个方向,那么解决这类问题一般可以从两个角度来做,一个就是利用几何性质,结合定理和推论来了得到,另一个就是建立直角坐标系,通过法向量和直线的方向向量来表示得到,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分13分)如图所示,四棱锥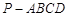 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,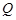 是棱
是棱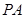 上的动点.
上的动点.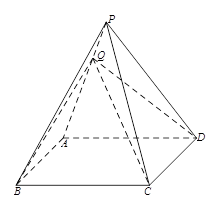
(Ⅰ)若 是
是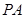 的中点,求证:
的中点,求证: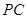 //平面
//平面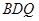 ;
;
(Ⅱ)若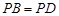 ,求证:
,求证: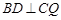 ;
;
(III)在(Ⅱ)的条件下,若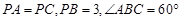 ,求四棱锥
,求四棱锥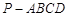 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,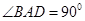 ,
,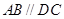 ,
, ,且PA=AD=DC=
,且PA=AD=DC=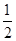 AB=1.
AB=1.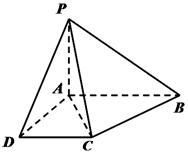
(1)证明:平面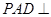 平面
平面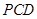
(2)设AB,PA,BC的中点依次为M、N、T,求证:PB∥平面MNT
(3)求异面直线 与
与 所成角的余弦值
所成角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图,四棱锥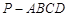 的底面
的底面 为菱形,
为菱形,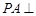 平面
平面 ,
,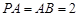 , E、F分别为
, E、F分别为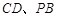 的中点,
的中点,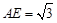 .
.
(Ⅰ)求证:平面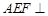 平面
平面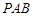 .
.
(Ⅱ)求平面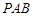 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.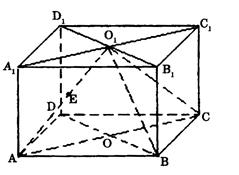
(1)求证:平面O1AC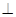 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在几何体ABCDE中,∠BAC=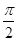 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1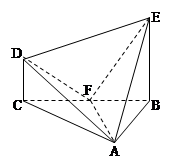
(Ⅰ)求证:DC∥平面ABE;
(Ⅱ)求证:AF⊥平面BCDE;
(Ⅲ)求证:平面AFD⊥平面AFE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com