
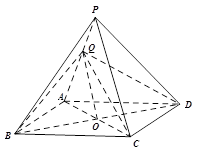
(本小题满分13分)如图所示,四棱锥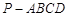 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,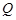 是棱
是棱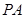 上的动点.
上的动点.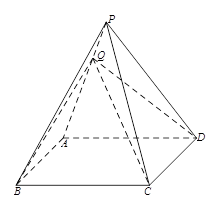
(Ⅰ)若 是
是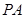 的中点,求证:
的中点,求证: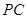 //平面
//平面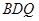 ;
;
(Ⅱ)若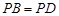 ,求证:
,求证: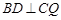 ;
;
(III)在(Ⅱ)的条件下,若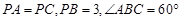 ,求四棱锥
,求四棱锥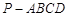 的体积.
的体积.
(1)根据底面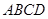 为菱形, 所以
为菱形, 所以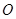 为
为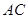 的中点.
的中点.
因为  是
是 的中点,所以
的中点,所以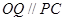 从而得证。
从而得证。
(2)根据已知的条件得到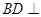 平面
平面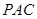 ,然后结合线面垂直的性质定理得到结论
,然后结合线面垂直的性质定理得到结论
(3)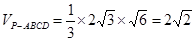
解析试题分析:(Ⅰ)证明:连结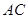 ,交
,交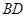 于
于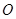 .
.
因为底面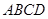 为菱形, 所以
为菱形, 所以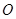 为
为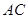 的中点.
的中点.
因为  是
是 的中点,所以
的中点,所以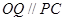 ,
,
因为 平面
平面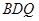 ,
,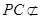 平面
平面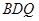 ,
,
所以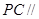 平面
平面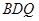 . …………………4分
. …………………4分
(Ⅱ)证明:因为底面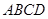 为菱形,
为菱形,
所以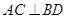 ,
, 为
为 的中点.
的中点.
因为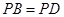 ,所以
,所以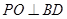 .
.
因为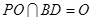 ,所以
,所以 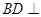 平面
平面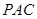 .因为
.因为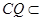 平面
平面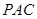 ,
,
所以 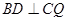 . ………………………………8分
. ………………………………8分
(Ⅲ)因为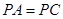 ,所以△
,所以△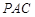 为等腰三角形 .
为等腰三角形 .
因为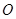 为
为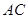 的中点,所以
的中点,所以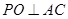 .
.
由(Ⅱ)知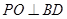 ,且
,且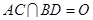 ,
,
所以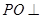 平面
平面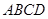 ,即
,即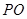 为四棱锥
为四棱锥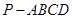 的高.
的高.
因为四边形是边长为2的菱形,且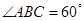 ,
,
所以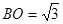
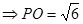 .
.
所以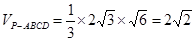 . ……………12分
. ……………12分
考点:线面平行,线线垂直,体积的问题
点评:解决该试题的关键是利用空间的线面平行和线面垂直的性质定理和判定定理来证明平行与垂直同时根据等体积法来求解体积。属于中档题。


科目:高中数学 来源: 题型:解答题
如图,正方形 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,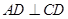 ,
, ∥
∥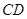 ,
,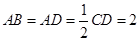 ,点
,点 在线段
在线段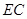 上.
上.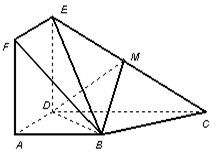
(I)当点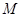 为
为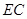 中点时,求证:
中点时,求证: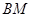 ∥平面
∥平面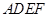 ;
;
(II)当平面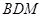 与平面
与平面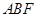 所成锐二面角的余弦值为
所成锐二面角的余弦值为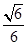 时,求三棱锥
时,求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,三棱锥P-ABC中,PC 平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD 平面PAB
平面PAB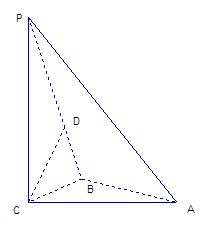
(1)求证:AB 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)如图,四边形ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.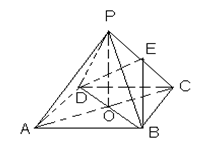
求证:(1) PA∥平面BDE .
(2)平面PAC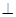 平面BDE .
平面BDE .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在四棱柱 中,底面
中,底面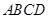 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC=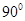 ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD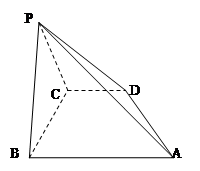
(1)求证:AB⊥平面PBC
(2)求三棱锥C-ADP的体积
(3)在棱PB上是否存在点M使CM∥平面PAD?
若存在,求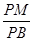 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com