练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，其左顶点在圆上.

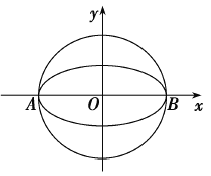
    （1）求椭圆的方程；

    （2）若点为椭圆上不同于点 的点，直线与圆的另一个交点为.是否存在点，使得?若存在，求出点的坐标；若不存在，说明理由.

    【答案】(1) (2) 不存在直线，使得

    【解析】

    （1）由题意求出a，通过离心率求出c，然后求解椭圆的标准方程；

    （2）设点，，设直线的方程为，与椭圆方程联立，利用弦长公式求出，利用垂径定理求出，从而整理即可得到结果.

    （1）因为椭圆的左顶点在圆上，令，得，所以，

    又离心率为，所以，所以，

    所以，

    所以的方程为.

    （2）设点，，设直线的方程为，

    与椭圆方程联立得

    化简得到，

    因为为方程的一个根，

    所以，所以，

    所以.

    因为圆心到直线的距离为，

    所以，

    因为，

    代入得到，

    显然，所以不存在直线，使得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

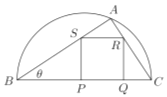
    【题目】校园准备绿化一块直径为的半圆形空地，点在半圆圆弧上，△外的地方种草，△的内接正方形为一水池（，在边上），其余地方种花，若， ，设△的面积为，正方形面积为；

    （1）用和表示和；

    （2）当固定，变化时，求最小值及此时的角；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某旅游风景区发行的纪念章即将投放市场，根据市场调研情况，预计每枚该纪念章的市场价y（单位：元）与上市时间x（单位：天）的数据如下：

    上市时间x天

    2

    6

    20

    市场价y元

    102

    78

    120

    （1）根据上表数据，从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由：①；②；③；

    （2）利用你选取的函数，求该纪念章市场价最低时的上市天数及最低的价格；

    （3）利用你选取的函数，若存在，使得不等式成立，求实数k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于的不等式（为实数）的解集为，集合.

    （1）若，求的取值范围；

    （2）若，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（个月）和市场占有率（）的几组相关对应数据：

    1

    2

    3

    4

    5

    0.02

    0.05

    0.1

    0.15

    0.18

    （1）根据上表中的数据，用最小二乘法求出关于的线性回归方程；

    （2）根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过（精确到月）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的参数方程为（为参数），，为曲线上的一动点.

    （I）求动点对应的参数从变动到时，线段所扫过的图形面积；

    （Ⅱ）若直线与曲线的另一个交点为，是否存在点，使得为线段的中点？若存在，求出点坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分，设在甲、乙的比赛中，每次发球，发球方得1分的概率为0.6，各次发球的胜负结果相互独立.甲、乙的一局比赛中，甲先发球.

    （1）求开始第4次发球时，甲、乙的比分为1比2的概率；

    （2）表示开始第4次发球时乙的得分，求的期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)求函数的最小值及取到最小值时自变量x的集合；

    (2)指出函数y＝的图象可以由函数y＝sinx的图象经过哪些变换得到；

    (3)当x∈[0，m]时，函数y＝f(x)的值域为，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，过且斜率为的直线交抛物线于，两点.若线段的垂直平分线与轴交于点，则（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案