
分析 由条件分别利用两角和差的正切公式、诱导公式、正弦定理,求得结论.
解答 解:(1)∵△ABC中,tanA=2,角C=45°,∴tanC=1,
∴tan(A+C)=$\frac{tanA+tanC}{1-tanAtanC}$=$\frac{2+1}{1-2×1}$=-3.
(2)tanB=-tan(A+C)=3.
(3)由(2)可得,tanB=$\frac{sinB}{cosB}$=3,sin2B+cos2B=1,∴sinB=$\frac{3\sqrt{10}}{10}$.
再根据正弦定理可得$\frac{AC}{sinB}$=$\frac{AB}{sinC}$,即 $\frac{AC}{\frac{3\sqrt{10}}{10}}$=$\frac{\sqrt{2}}{\frac{\sqrt{2}}{2}}$,∴AC=$\frac{3\sqrt{10}}{5}$.
点评 本题主要考查两角和差的正切公式、诱导公式、正弦定理,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x}$ | B. | y=-sinx | C. | $y=\frac{1}{x}$ | D. | $y=\frac{{{x^2}-1}}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
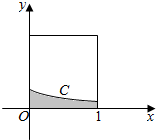 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )| A. | 1193 | B. | 1359 | C. | 2718 | D. | 3413 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
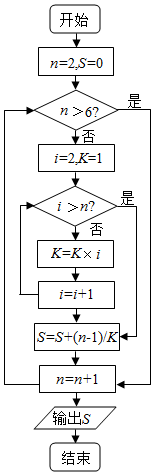
| A. | $\frac{119}{120}$ | B. | $\frac{359}{360}$ | C. | $\frac{719}{720}$ | D. | $\frac{5039}{5040}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
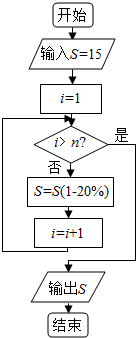 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )| A. | 9.6 | B. | 7.68 | C. | 6.144 | D. | 4.9152 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com