
 矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )| A. | $[0,\frac{π}{6}]$ | B. | $[0,\frac{π}{3}]$ | C. | $[0,\frac{π}{2}]$ | D. | $[0,\frac{2π}{3}]$ |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{\sqrt{2e}}}{2e}+1)$ | B. | $(1,\frac{1}{e}+1)$ | C. | $(0,\frac{1}{2e}+1)$ | D. | $(\frac{1}{e},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
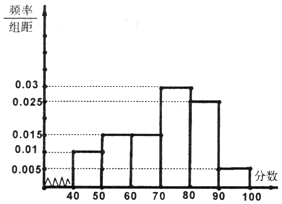 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x|+1 | B. | y=$\frac{1}{x}$ | C. | y=-x2+1 | D. | y=-x|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com