
分析 由正弦定理可得$sinCsinA=\sqrt{3}sinAcosC$,从而得到$tanC=\sqrt{3},C=\frac{π}{3}$,由$\frac{1}{2}absinC=\frac{{3\sqrt{3}}}{2}$,得ab=6,由此利用余弦定理能求出a+b.
解答 解:∵在△ABC中,角A,B,C所对的边分别为a,b,c,已知$csinA=\sqrt{3}acosC$,
∴由正弦定理可得$sinCsinA=\sqrt{3}sinAcosC$,
解得$tanC=\sqrt{3},C=\frac{π}{3}$,
∴$\frac{1}{2}absinC=\frac{{3\sqrt{3}}}{2}$,解得ab=6,
∵$c=\sqrt{31}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
∴$\frac{1}{2}=\frac{{a}^{2}+\frac{36}{{a}^{2}}-31}{2×6}$,解得a=1,b=6或a=6,b=1,
∴a+b=7.
故答案为:$\frac{π}{3}$,7.
点评 本题考查三角形的角及边长的求法,涉及到正弦定理、余弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2ln2-2-(ln2)3 | B. | -1 | C. | 2ln2-2-(ln2)2k | D. | (k-1)ek-k3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 、$-\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
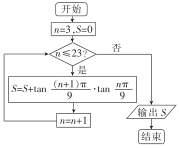
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com