
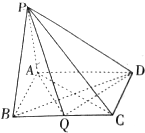
 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).分析 (1)由线面垂直得AC⊥PD,由正方形性质得AC⊥BD,由此能证明平面PAC⊥平面PBD.
(2)由已知中PA⊥平面ABCD,四边形ABCD为矩形,我们易得PQ⊥QD?AQ⊥QD,由此我们易得以AD为半径的圆与BC应该有交点,即可得到满足条件的实数a的值范;取AD的中点M,过M作MN⊥PD,垂足为N,连接QM,QN,根据三垂线定理,我们易判断出∠QNM为二面角Q-PD-A的平面角,解三角形QMN,即可得到二面角Q-PD-A的余弦值大小.
解答  (1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
(1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD,…(4分)
又AC?平面PAC,
∴平面PAC⊥平面PBD;
(2)解:∵PA⊥平面ABCD,
∴PA⊥QD,若PQ⊥QD成立,即AQ⊥QD成立,
∴点Q应为BC与以AD为直径的圆的公共点,
∴当a=$\frac{1}{2}$时,BC上有且仅有一点满足题意,此时Q点为BC的中点,
取AD的中点M,过M作MN⊥PD,垂足为N,连接QM,QN,
由于QN⊥平面PAD,
∴∠QNM为二面角Q-PD-A的平面角,
设AB=1,则MD=1,PD=$\sqrt{5}$,且△DNM∽△DAP,
∴MN=$\frac{1}{\sqrt{5}}$,
从而在直角△QNM中,QN=$\frac{\sqrt{6}}{\sqrt{5}}$,
∴cos∠QNM=$\frac{MN}{QN}$=$\frac{\sqrt{6}}{6}$.
点评 本题考查平面与平面垂直的证明,考查二面角大小的求法,(2)的关键是求出二面角Q-PD-A的平面角.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{{4\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=( )
某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=( )| A. | 219 | B. | 211 | C. | 209 | D. | 213 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com