练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．某同学做了一个如图所示的等腰直角三角形形状的数表，且把奇数和偶数分别依次排在了数表的奇数行和偶数行，若用a（i，j）表示第i行从左数第j个数，如a（4，3）=10，则a（21，6）=（　　）
    A．219B．211C．209D．213

    分析 由三角形数表可以看出其奇数行为奇数列，偶数行为偶数列，故a（21，6）对应的数字为奇数，分析对应数字与行列的关系，可得答案．

    解答 解：由三角形数表可以看出其奇数行为奇数列，偶数行为偶数列，
    故a（21，6）对应的数字为奇数，
    由前面奇数行共有；1+3+5+…+19=100个奇数，
    故a（21，6）为第106个奇数，
    由2×106-1=211，
    可得a（21，6）=211，
    故选：B

    点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

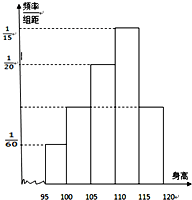    12．某幼儿园中班共36个小朋友的身高（单位：厘米）测量结果如下频率
    分布直方图所示，该班小朋友牛牛的身高118cm，他所在的身高段共有6个小朋友．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．某天连续有7节课，其中语文、英语、物理、化学、生物5科各1节，数学2节．在排课时，要求生物课不排第1节，数学课要相邻，英语课与数学课不相邻，则不同排法的种数是（　　）
    A．408B．480C．552D．816

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

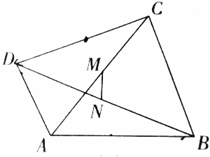    9．如图，四边形ABCD的对角线AC、BD的中点分别为M、N，求证：$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$（AB+CD）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

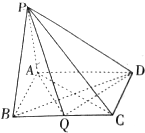    16．在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为矩形，AB=PA=aBC（a＞0）．
    （1）当a=1时，求证：平面PBD⊥平面PAC；
    （2）试问BC边上是否存在唯一的点Q，使得PQ⊥QD．若存在，求此时a的值及二面角A-PD-Q的余弦值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设f（x）是偶函数，且当x≥0时，f（x）=$\left\{\begin{array}{l}x（3-x），0≤x≤3\\（x-3）（a-x），x＞3\end{array}$．
    （1）当a=5时，判断f（x）=1有几个不同的实数根，说明理由；
    （2）设函数f（x）在区间[-5，5]上最大值为g（a），试求g（a）的表达式；
    （3）若方程f（x）=m恰有四个不同的实根x1，x2，x3，x4，x1＜x2＜x3＜x4，且它们依次构成等差数列，求a的取值范围及m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．方程sinx+$\sqrt{3}$cosx+a=0在（0，π）内有两个不同的解α、β，求：
    （1）a的范围；
    （2）α+β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知点P（1，2），Q（2cosα，2sinα），则|$\overrightarrow{PQ}$|的取值范围是[$\sqrt{5}-2$，$2+\sqrt{5}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．二项式$（\frac{1}{{\sqrt{x}}}-{x^2}{）^{10}}$的展开式中的常数项是（　　）
    A．-45B．-10C．45D．65

    查看答案和解析>>

    同步练习册答案