
分析 设出直线方程$\frac{x}{a}+\frac{y}{b}=1$(a<0,b<0),把点P坐标代入,求出直线在两坐标轴上的截距,结合直线与两坐标轴在第三象限围成三角形面积为5列式求得a,b的值得答案.
解答 解:设所求直线方程为$\frac{x}{a}+\frac{y}{b}=1$(a<0,b<0),
由直线过点P(-5,-4),得$\frac{-5}{a}+\frac{-4}{b}=1$,∴4a+5b=-ab,①
又$\frac{1}{2}$|ab|=5,②
联立①②得:$a=-\frac{5}{2},b=-4$.
∴所求直线方程为:$\frac{x}{-\frac{5}{2}}+\frac{y}{-4}=1$,即8x+5y+20=0.
故答案为:8x+5y+20=0.
点评 本题考查直线方程的求法,考查了直线方程的截距式,是基础题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
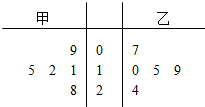 某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.
某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
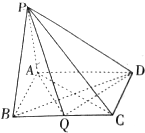 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com