Question

2．在△ABC中，AC=2AB=2，BC=$\sqrt{3}$，P是△ABC内部的一点，若∠APB=∠BPC=∠CPA，则PA+PB+PC=$\sqrt{7}$．

Answer 1

分析 由∠APB=∠BPC=∠CPA=120°，∠ACB=60°，可以得到∠ACP=∠PBC，判定两个三角形相似，然后用相似三角形的性质计算求出PB、PC的长，再利用余弦定理求出PA，即可得出结论．

解答 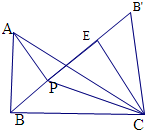解：延长BP到B′，在BB'上取点E，使PE=PC，EB′=AP，
∵∠BPC=120°，
∴∠EPC=60°，
∴△PCE是正三角形，
∴∠CEB'=120°=∠APC
∵AP=EB′，PC=EC，
∴PC=CE，
∴△ACP≌△B′CE，
∴∠PCA=∠B′CE，AC=B′C=2
∴∠PCA+∠ACE=∠ACE+∠ECP
∴∠ACB′=∠PCE=60°，
∵AC=2AB=2，BC=$\sqrt{3}$，
∴AC²=BC²+AB²，
∴∠ABC=90°，∠ACB=30°
∴∠BCB′=90°，
∵PE=PC，AP=B′E
∴PA+PB+PC=PA+EP+B′E=BB′=$\sqrt{B{C}^{2}+BB{′}^{2}}$=$\sqrt{7}$，
故答案为：$\sqrt{7}$．

点评 本题考查的是相似三角形的判定与性质，考查余弦定理，考查学生的计算能力，属于中档题．