
| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
分析 利用向量的坐标运算得到|2$\overrightarrow a-\overrightarrow b|$用θ的三角函数表示化简求最值.
解答 解:向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow b=(\sqrt{3},-1)$,则2$\overrightarrow{a}-\overrightarrow{b}$=(2cosθ-$\sqrt{3}$,2sinθ+1),
所以|2$\overrightarrow a-\overrightarrow b|$2=(2cosθ-$\sqrt{3}$)2+(2sinθ+1)2=8-4$\sqrt{3}$cosθ+4sinθ=8-8sin($θ-\frac{π}{3}$),
所以|2$\overrightarrow a-\overrightarrow b|$2的最大值,最小值分别是:16,0;
所以|2$\overrightarrow a-\overrightarrow b|$的最大值,最小值分别是4,0;
故选:A.
点评 本题考查了向量的坐标运算以及三角函数解析式的化简;利用了两角差的正弦公式以及正弦函数的有界性.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
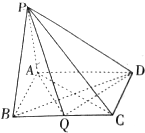 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -45 | B. | -10 | C. | 45 | D. | 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | [-1,1] | C. | (1,5] | D. | [1,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±3x | B. | y=±2$\sqrt{2}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com