
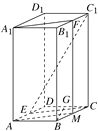
【题目】(2017·泰安模拟)如图,在正四棱柱ABCDA1B1C1D1中,E为AD的中点,F为B1C1的中点.
(1)求证:A1F∥平面ECC1;
(2)在CD上是否存在一点G,使BG⊥平面ECC1?若存在,请确定点G的位置,并证明你的结论,若不存在,请说明理由.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1) 取BC的中点M,易得A1F∥AM, ,CE∥AM,所以CE∥A1F.再根据线面平行判定定理得结论 (2) 作BG⊥EC.则G为CD的中点时,由线面垂直性质得CC1⊥BG.再根据线面垂直判定定理得结论
试题解析:解:(1)证明:如图,在正四棱柱ABCDA1B1C1D1中,取BC的中点M,连接AM,FM,
所以B1F∥BM且B1F=BM,
所以四边形B1FMB是平行四边形,
所以FM∥B1B且FM=B1B.
因为B1B∥A1A且B1B=A1A,
所以FM∥A1A且FM=A1A,
所以四边形AA1FM是平行四边形,所以A1F∥AM.
因为E为AD的中点,
所以AE∥MC且AE=MC.
所以四边形AMCE是平行四边形,
所以CE∥AM,所以CE∥A1F.
因为A1F平面ECC1,EC平面ECC1,
所以A1F∥平面ECC1.
(2)在CD上存在一点G,使BG⊥平面ECC1.
证明如下:取CD的中点G,连接BG.
在正方形ABCD中,DE=GC,CD=BC,∠ADC=∠BCD,
所以△CDE≌△BCG,
所以∠ECD=∠GBC.
因为∠CGB+∠GBC=90°,
所以∠CGB+∠DCE=90°,所以BG⊥EC.
因为CC1⊥平面ABCD,BG平面ABCD,
所以CC1⊥BG.又EC∩CC1=C,
所以BG⊥平面ECC1.
故当G为CD的中点时,满足BG⊥平面ECC1.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)当![]() (
(![]() )时在曲线
)时在曲线![]() 上对应的点为
上对应的点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的极坐标,并判断
点的极坐标,并判断![]() 是否在曲线
是否在曲线![]() 上(其中点
上(其中点![]() 为半圆的圆心)
为半圆的圆心)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.

(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·贵州适应性考试)如图,在正方体ABCDA1B1C1D1中,点P是线段A1C1上的动点,则三棱锥PBCD 的俯视图与正视图面积之比的最大值为( )

A. 1 B. ![]()
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为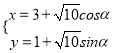 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程,并说明其表示什么轨迹;
的极坐标方程,并说明其表示什么轨迹;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为4,椭圆
的距离为4,椭圆![]()
![]() 的离心率
的离心率![]() ,且过抛物线的焦点
,且过抛物线的焦点![]() .
.
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两不同点,交
两不同点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
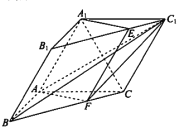
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且在
有极值,且在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .若存在,求出实数
.若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com