
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 用“条件约束函数”的定义加以验证,对于①③④均可以找到常数ω>0,使|f(x)|≤ω|x|对一切实数x均成立,说明它们是F函数,
而对于②,所以不存在常数ω>0,使|f(x)|≤ω|x|对一切实数x均成立,故它们不符合题意.
解答 解:对于①,f(x)=4x,易知ω=4符合题意,
①是“条件约束函数”,
对于②,用“条件约束函数”的定义不难发现:因为x→0时,|$\frac{f(x)}{x}$|→∞,
所以不存在常数ω>0,使|f(x)|≤ω|x|对一切实数x均成立,
②不是“条件约束函数”,
对于③,因为|f(x)|=$\frac{2|x|}{{(x-1)}^{2}+4}$≤$\frac{1}{2}$|x|,
所以存在常数ω=$\frac{1}{2}$>0,使|f(x)|≤ω|x|对一切实数x均成立,
③是“条件约束函数”函数,
对于④,f(x)是定义在实数集R上的奇函数,故|f(x)|是偶函数,
因而由|f(x1)-f(x2)|≤4|x1-x2|得到,|f(x)|≤4|x|成立,
存在ω≥4>0,使|f(x)|≤ω|x|对一切实数x均成立,符合题意,
④是“条件约束函数”,
故选:C.
点评 本题考查了函数的定义域和值域的问题,属于中档题.题中“条件约束函数”的实质是函数f(x)与x的比值对应的函数是有界的,抓住这一点我们不难解出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
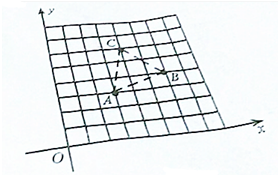 如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com