
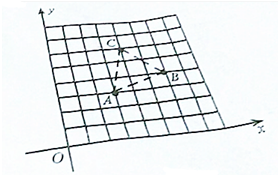
 如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6). 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知a,b∈R,则“$\frac{{{a^2}+{b^2}}}{ab}≤-2$”是“a>0且b<0”的充分不必要条件 | |
| B. | 已知数列{an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | 已知两个平面α,β,若两条异面直线m,n满足m?α,n?β且m∥β,n∥α,则α∥β | |
| D. | ?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com