
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知偶函数![]() 满足
满足![]() ,现给出下列命题:①函数
,现给出下列命题:①函数![]() 是以2为周期的周期函数;②函数
是以2为周期的周期函数;②函数![]() 是以4为周期的周期函数;③函数
是以4为周期的周期函数;③函数![]() 为奇函数;④函数
为奇函数;④函数![]() 为偶函数,则其中真命题的个数是( )
为偶函数,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记
年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了![]() 名学生的考核成绩,并作成如下茎叶图:
名学生的考核成绩,并作成如下茎叶图:
5 | 0 | 1 | 1 | 6 | ||||
6 | 0 | 1 | 4 | 3 | 3 | 5 | 8 | |
7 | 2 | 3 | 7 | 6 | 8 | 7 | 1 | 7 |
8 | 1 | 1 | 4 | 5 | 2 | 9 | ||
9 | 0 | 2 | 1 | 3 | 0 |
(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取
的学生中任取![]() 人,求至少有一人考核优秀的概率;
人,求至少有一人考核优秀的概率;
(Ⅲ)记![]() 表示学生的考核成绩在区间
表示学生的考核成绩在区间![]() 内的概率,根据以往培训数据,规定当
内的概率,根据以往培训数据,规定当![]() 时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法:
①回归直线可以不过样本的中心点;
②在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程![]() 中,当解释变量x每增加一个单位时,预报变量
中,当解释变量x每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量X与Y,若它们的随机变量![]() 的观测值k越小,则判断“X与Y有关系”的把握程度越大.
的观测值k越小,则判断“X与Y有关系”的把握程度越大.
其中正确的说法是( )
A.①④B.②③C.①③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批用于手电筒的电池,每节电池的寿命服从正态分布![]() (寿命单位:小时).考虑到生产成本,电池使用寿命在
(寿命单位:小时).考虑到生产成本,电池使用寿命在![]() 内是合格产品.
内是合格产品.
(1)求一节电池是合格产品的概率(结果四舍五入,保留一位小数);
(2)根据(1)中的数据结果,若质检部门检查4节电池,记抽查电池合格的数量为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望及方差.
的分布列、数学期望及方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月23日,在![]() 省
省![]() 市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量
市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量![]() (单位:
(单位:![]() )与每日营养液注射量
)与每日营养液注射量![]() (单位:
(单位:![]() )之间的关系统计出表1一组数据:
)之间的关系统计出表1一组数据:
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根据表1和表2的相关统计值求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)计算拟合指数![]() 的值,并说明线性回归模型的拟合效果(
的值,并说明线性回归模型的拟合效果(![]() 的值在.98以上说明拟合程度好);
的值在.98以上说明拟合程度好);
(3)若某日该农产品的营养液注释量为![]() ,预测该日这种农产品的平均增长重量(结果精确到0.1).
,预测该日这种农产品的平均增长重量(结果精确到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: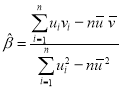 ,
,![]() ,
,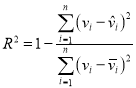 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.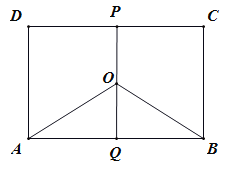
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com