
【题目】已知函数![]() 与
与![]() 都是定义在
都是定义在![]() 上的奇函数, 当
上的奇函数, 当![]() 时,
时,![]() ,则
,则![]() (4)的值为____.
(4)的值为____.
【答案】2
【解析】
根据题意,由f(x﹣1)是定义在R上的奇函数可得f(x)=﹣f(﹣2﹣x),结合函数为奇函数,分析可得f(x)=f(x﹣2),则函数是周期为2的周期函数,据此可得f(![]() )=f(
)=f(![]() )=﹣f(
)=﹣f(![]() ),结合函数的解析式可得f(
),结合函数的解析式可得f(![]() )的值,结合函数的奇偶性与周期性可得f(0)的值,相加即可得答案.
)的值,结合函数的奇偶性与周期性可得f(0)的值,相加即可得答案.
根据题意,f(x﹣1)是定义在R上的奇函数,则f(x)的图象关于点(﹣1,0)对称,
则有f(x)=﹣f(﹣2﹣x),
又由f(x)也R上的为奇函数,则f(x)=﹣f(﹣x),且f(0)=0;
则有f(﹣2﹣x)=f(﹣x),即f(x)=f(x﹣2),
则函数是周期为2的周期函数,
则f(![]() )=f(
)=f(![]() )=﹣f(
)=﹣f(![]() ),又由f(
),又由f(![]() )=log2(
)=log2(![]() )=﹣2,则f(
)=﹣2,则f(![]() )=2,
)=2,
f(4)=f(0)=0,
故f(![]() )+f(4)=2+0=2;
)+f(4)=2+0=2;
故答案为:2.


科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
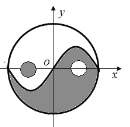
【题目】太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆![]() 被
被![]() 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为
的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为![]() ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,正确的题号是__________.
①函数的最值一定是极值;
②设![]() :实数
:实数![]() ,
,![]() 满足
满足![]() ;
;![]() :实数
:实数![]() ,
,![]() 满足
满足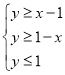 ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③已知椭圆![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的离心率,则
的离心率,则![]() ,且
,且![]() ;
;
④一动圆![]() 过定点
过定点![]() ,且与已知圆
,且与已知圆![]() :
:![]() 相切,则动圆圆心
相切,则动圆圆心![]() 的轨迹方程是
的轨迹方程是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市民用水拟实行阶梯水价,每人用水量中不超过![]() 立方米的部分按4元/立方米收费,超出
立方米的部分按4元/立方米收费,超出![]() 立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
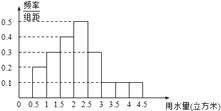
(1)如果![]() 为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,
为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米, ![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,估计该市居民该月的人均水费.
时,估计该市居民该月的人均水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com