练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知A={x|x2+3x-10≤0}，B={x|m+1≤x≤2m-1}，B⊆A，求m的取值范围．

    分析 先化简集合A，由B⊆A得B=∅，或m≥2时，由B⊆A，得$\left\{\begin{array}{l}{m+1≥-5}\\{2m-1≤2}\end{array}\right.$，解得即可．

    解答 解：∵x2+3x-10≤0，∴（x-2）（x+5）≤0，解得-5≤x≤2．∴A={x|-5≤x≤2}．
    ∵B⊆A，
    ∴B=∅时，m+1＞2m-1，即m＜2；
    B≠∅，m+1≤2m-1，即m≥2时，由B⊆A，得$\left\{\begin{array}{l}{m+1≥-5}\\{2m-1≤2}\end{array}\right.$，即-6≤m≤1.5，不符合；
    综上所述m＜2；．

    点评 本题考查了集合间的关系，分类讨论和数形结合是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．若函数f（x）=$\sqrt{{x^2}+2ax-a}$的定义域为R，则a的取值范围为[-1，0]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在△ABC中，a=$\sqrt{3}$，b=3，sinC=2sinA，则cosA=$\frac{{\sqrt{3}}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．6名同学站成一排照毕业相，要求甲不站在两侧，而且乙和丙相邻、丁和戊相邻，则不同的站法种数为（　　）
    A．60B．96C．48D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）=ax2-2ax+c满足f（2017）＜f（-2016），则满足f（m）≤f（0）的实数m的取值范围是（　　）
    A．（-∞，0]B．[0，2]C．（-∞，0]∪[2，+∞）D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设f（x）=logax（a＞0，a≠1）．若f（x1x2…x2017）=6，则f（x13）+f（x23）+…+f（x20173）=（　　）
    A．64B．4C．18D．2$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若三棱台ABC-A1B1C1中，AB=6，A1B1=3，则三棱锥A-A1B1C1与三棱锥B1-ABC的体积之比是$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

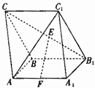    9．已知三棱柱ABC-A1B1C1中，侧面AA1B1B⊥侧面BB1C1C，且侧面AA1B1B为正方形，侧面BB1C1C为菱形，∠BB1C1=60°．
    （1）求证：B1C⊥AC1；
    （2）若点E是B1C的中点，点F是AA1的中点，求证：EF∥平面ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若数列{an}中，a1=1，an+an-1=3（n≥2），Sn为数列{an}的前n项和，则S2015=3022．

    查看答案和解析>>

    同步练习册答案