练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．6名同学站成一排照毕业相，要求甲不站在两侧，而且乙和丙相邻、丁和戊相邻，则不同的站法种数为（　　）
    A．60B．96C．48D．72

    分析 根据题意，分3步进行分析，①、因为乙和丙相邻，用捆绑法分析可得其情况数目，②、丁和戊相邻，同理可得情况数目，③、将这两个整体与剩下的2人排列，因为甲不站在两侧，则甲有2个位置可选，分析可得其情况数目，进而由分步计数原理计算可得答案．

    解答 解：根据题意，分3步进行分析，
    ①、因为乙和丙相邻，将其看成一个整体，考虑两人的顺序，有A22=2种情况，
    ②、同理，丁和戊相邻，也有2种情况，
    ③、将这两个整体与剩下的2人排列，因为甲不站在两侧，则甲有2个位置可选，则共有2×A33=12种情况，
    则不同的站法种数为2×2×12=48种；
    故选：C．

    点评 本题考查排列、组合的运用，因为涉及的限制条件比较多，所以注意认真分析题意，认清问题是排列还是组合问题，还要注意相邻问题需要用捆绑法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知集合A={x|1-a≤x≤a+1}，B={x|x2-3x-4≥0}，若A∩B=∅，则实数a的取值范围为（　　）
    A．（-∞，-1）B．（-∞，2）C．（0，2）D．[0，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙，已知从城市甲到城市乙只有两条公路，且通过这两条公路所用的时间互不影响．据调查统，通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如表：
    所用的时间（天数）10111213
    通过公路l的频数20402020
    通过公路2的频数10404010
    假设汽车A只能在约定日期（某月某日）的前11天出发，汽车B只能在约定日期的前12天出发（将频率视为概率）．
    （I）为了尽最大可能在各自允许的时间内将货物运往城市乙，估计汽车A和汽车B应如何选择各自的路径；
    （Ⅱ）若通过公路l、公路2的“一次性费用”分别为3.2万元、1.6万元（其他费用忽略不计），此项费用由生产商承担．如果生产商恰能在约定日期当天将货物送到，则销售商一次性支付给生产商40万元，若在约定日期前送到；每提前一天销售商将多支付给生产商2万元；若在约定日期后送到，每迟到一天，生产商将支付给销售商2万元．如果汽车A，B按（I）中所选路径运输货物，试比较哪辆汽车为生产商获得的毛利润更大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图，平面上有四个点A、B、P、Q，其中A、B为定点，且AB=$\sqrt{3}$，P、Q为动点，满足AP=PQ=QB=1，又△APB和△PQB的面积分别为S和T，则S2+T2的最大值为$\frac{7}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．如图所示正方形O'A'B'C'的边长为2cm，它是一个水平放置的一个平面图形的直观图，则原图形的面积是4$\sqrt{2}$cm2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．组数据2，x，4，6，10的平均值是5，则此组数据的方差是8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知A={x|x2+3x-10≤0}，B={x|m+1≤x≤2m-1}，B⊆A，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合A是由0，m，m2-3m+2三个元素组成的集合，且2∈A，则实数m的值为（　　）
    A．2B．3C．0或3D．0或2或3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

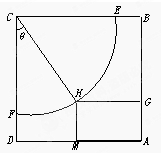    18．某体育馆拟用运动场的边角地建一个矩形的健身室（如图所示），ABCD是一个标出为50m的正方形地皮，扇形CEF是运动场的一部分，其半径为40m，矩形AGHM就是拟建的健身室，其中G，M分别在AB和AD上，H在$\widehat{EF}$上，设矩形AGHM的面积为S，∠HCF=θ．
    （I）请将S表示为θ的函数，并指出当点H在$\widehat{EF}$的何处时，该健身室的面积最大，最大面积是多少？
    （Ⅱ）由上面函数建立的思想，试求$f（x）=x\sqrt{4-{x^2}}$的最大值．

    查看答案和解析>>

    同步练习册答案