
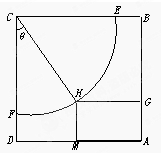
 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一个标出为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G,M分别在AB和AD上,H在$\widehat{EF}$上,设矩形AGHM的面积为S,∠HCF=θ.
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一个标出为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G,M分别在AB和AD上,H在$\widehat{EF}$上,设矩形AGHM的面积为S,∠HCF=θ.分析 (I)延长GH交CD于N,则NH=40sinθ,CH=40cosθ,求出S的表达式,通过换元法,利用正弦函数的有界性求解即可.
(II)设x=2cosθ,θ∈[0,π],三角换元则函数化求解函数的最值.
解答 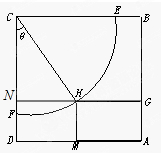 解:(I)延长GH交CD于N,则NH=40sinθ,CH=40cosθ,
解:(I)延长GH交CD于N,则NH=40sinθ,CH=40cosθ,
∴HM=ND=50-40cosθ,AM=50-40sinθ,
故S=(50-40cosθ)(50-40sinθ)
=$100[{25-20({sinθ+cosθ})+16sinθcosθ}]({0≤θ≤\frac{π}{2}})$.
令$t=sinθ+cosθ=\sqrt{2}sin({θ+\frac{π}{4}})$,则$sinθcosθ=\frac{{{t^2}-1}}{2}$,且$t∈[{1,\sqrt{2}}]$∴$S=100[{25-20t+8{{({t-1})}^2}}]=800{({t-\frac{5}{4}})^2}+450$
又$t∈[{1,\sqrt{2}}]$,∴当t=1时,Smax=500,此时$\sqrt{2}sin({θ+\frac{π}{4}})=1⇒sin({θ+\frac{π}{4}})=\frac{{\sqrt{2}}}{2}$∵$\frac{π}{4}≤θ+\frac{π}{4}≤\frac{3π}{4}∴θ+\frac{π}{4}=\frac{π}{4}$或$\frac{3π}{4}$,即θ=0或$θ=\frac{π}{2}$;
(II)设x=2cosθ,θ∈[0,π],三角换元则函数化为$y=2cosθ•\sqrt{4-{{({2cosθ})}^2}}=2cosθ•2sinθ=2sin2θ$,
∴ymax=2.
点评 本题考查三角函数的有界性的应用,换元法求解函数的最值,考查转化思想以及计算能力.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
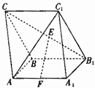 已知三棱柱ABC-A1B1C1中,侧面AA1B1B⊥侧面BB1C1C,且侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠BB1C1=60°.
已知三棱柱ABC-A1B1C1中,侧面AA1B1B⊥侧面BB1C1C,且侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠BB1C1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | $\frac{1}{9}$ | C. | 10 | D. | D、不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com