
分析 (Ⅰ)由已知求出原函数的导函数,再由f′(1)=$-\frac{1}{2}$求得a值,得到函数解析式,求出f(1),利用直线方程的点斜式得答案;
(Ⅱ)依题可知方程f′(x)=m+2有三个不同实根,即:$\frac{1}{2}{x}^{2}-3x+2lnx=m$有三个不同实根.设h(x)=$\frac{1}{2}{x}^{2}-3x+2lnx$,由导数可知h(x)极小值h(2)=2ln2-4;极大值为h(1)=$-\frac{5}{2}$.则h(x)=m三个实根满足0<x1<1<x2<2<x3,再设h1(x)=h(x)-h(2-x),x∈(0,1),由导数得到x1+x2>2,设h2(x)=h(x)-h(4-x),x∈(1,2),由导数得到x3+x2<4,联立可得可得x3-x1<2.
解答 (Ⅰ)解:由已知f′(x)=$\frac{1}{2}{x}^{2}+ax+2lnx+2$,则f′(1)=$\frac{1}{2}+a+2=-\frac{1}{2}$,得a=-3,
∴f(x)=$\frac{{x}^{3}}{6}-\frac{3}{2}{x}^{2}+2xlnx$,则f(1)=$\frac{1}{6}-\frac{3}{2}=-\frac{4}{3}$,
∴切线方程为:y+$\frac{4}{3}=-\frac{1}{2}(x-1)$,即:3x+6y+5=0;
(Ⅱ)证明:依题可知方程f′(x)=m+2有三个不同实根,即:$\frac{1}{2}{x}^{2}-3x+2lnx=m$有三个不同实根.
设h(x)=$\frac{1}{2}{x}^{2}-3x+2lnx$,则h′(x)=x-3+$\frac{2}{x}$=$\frac{{x}^{2}-3x+2}{x}=\frac{(x-1)(x-2)}{x}$,
∴x∈(0,1)时,h(x)单调递增,x∈(1,2)时,h(x)单调递减,x∈(2,+∞)时,h(x)单调递增,
∴h(x)极小值h(2)=2ln2-4;极大值为h(1)=$-\frac{5}{2}$.
h(x)=m三个实根满足0<x1<1<x2<2<x3,
设h1(x)=h(x)-h(2-x),x∈(0,1),
h1′(x)=h′(x)+h′(2-x)=$\frac{4(x-1)^{2}}{x(2-x)}$>0,则h1(x)<h1(1)=h(1)-h(2-1)=0,
即h(x)<h(2-x),x∈(0,1),
∴f(x2)=f(x1)<f(2-x1),
∵函数h(x)在(1,2)上单调递减,从而x2>2-x1,即x1+x2>2,①
同理设h2(x)=h(x)-h(4-x),x∈(1,2),h2′(x)=h′(x)+h′(4-x)=$\frac{2(x-2)^{2}}{x(4-x)}$>0,则h2(x)<h2(2)=h(2)-h(4-2)=0,
即h(x)<h(4-x),x∈(1,2),
∴f(x3)=f(x4)<f(4-x2),
∵函数f(x)在(2,+∞)上单调递增,从而x3<4-x2,即x3+x2<4,②
由①②可得x3-x1<2.
点评 本题考查导数在研究函数的切线中的应用,考查导数在研究函数的单调性中的应用,构造函数并由函数的单调性得到x1+x2>2,x3+x2<4是解答该题的关键,难度较大.


科目:高中数学 来源: 题型:解答题
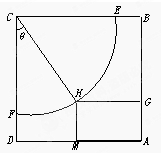 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一个标出为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G,M分别在AB和AD上,H在$\widehat{EF}$上,设矩形AGHM的面积为S,∠HCF=θ.
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一个标出为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G,M分别在AB和AD上,H在$\widehat{EF}$上,设矩形AGHM的面积为S,∠HCF=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 3:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m?α,n∥m⇒n∥α | B. | m?α,n⊥m⇒n⊥α | C. | m⊥α,m∥n,n∥β⇒α⊥β | D. | m?α,n?β,m∥n⇒α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com