
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 由题意可得 $\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$+0=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ,由此求得cosθ的值,可得θ的值.
解答 解:向量$\overrightarrow a$=(1,0),$\overrightarrow b$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,则$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$+0=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=1•1•cosθ,
∴cosθ=-$\frac{1}{2}$,∴θ=120°,
故选:C.
点评 本题主要考查两个向量的数量积公式,两个向量的数量积的定义,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2+1 | B. | y=1-$\frac{1}{x}$ | C. | y=x2-5x-6 | D. | y=3-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图直角梯形OABC中,$∠COA=∠OAB=\frac{π}{2},OC=2,OA=AB=1,SO⊥$面OABC,SO=1,以OC,OA,OS分别为x轴,y轴,z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,$∠COA=∠OAB=\frac{π}{2},OC=2,OA=AB=1,SO⊥$面OABC,SO=1,以OC,OA,OS分别为x轴,y轴,z轴建立直角坐标系O-xyz.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
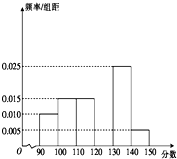 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )| A. | 121 | B. | 119 | C. | 118.5 | D. | 118 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
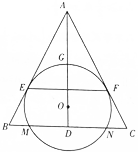 如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.
如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com