
分析 将已知两式子相加可解得:c=$\frac{{b}^{2}+1}{4}$,相减可得a=$\frac{{b}^{2}-2\sqrt{3}b-1}{4}$=$\frac{(b-\sqrt{3})^{2}}{4}$-1>0,显然c>a,解得:b>2+$\sqrt{3}$,或b<$\sqrt{3}-2$<0(舍去),再由c-b=$\frac{{b}^{2}+1}{4}$-b=$\frac{(b-2)^{2}}{4}$>0(b>2+$\sqrt{3}$),可得最大边为c,由余弦定理可得:($\frac{{b}^{2}+1}{4}$)2=($\frac{{b}^{2}-2\sqrt{3}b-1}{4}$)2+b2-2×$\frac{{b}^{2}-2\sqrt{3}b-1}{4}$×b×cosC,化简可解得cosC的值.
解答 解:∵b2-2a-$\sqrt{3}$b-2c=0,①
2a+$\sqrt{3}$b-2c+1=0,②
∴①+②可解得:c=$\frac{{b}^{2}+1}{4}$,
①-②可解得:a=$\frac{{b}^{2}-2\sqrt{3}b-1}{4}$=$\frac{(b-\sqrt{3})^{2}}{4}$-1>0,
∴显然c>a,解得:|b-$\sqrt{3}$|>2,即:b>2+$\sqrt{3}$,或b<$\sqrt{3}-2$<0(舍去),
再比较c与b的大小.
∵c-b=$\frac{{b}^{2}+1}{4}$-b=$\frac{{b}^{2}+1-4b}{4}$=$\frac{(b-2)^{2}}{4}$>0(b>2+$\sqrt{3}$).
∴c>b,
∴最大边为c.
由余弦定理可得 c2=a2+b2-2ab•cosC,
即:($\frac{{b}^{2}+1}{4}$)2=($\frac{{b}^{2}-2\sqrt{3}b-1}{4}$)2+b2-2×$\frac{{b}^{2}-2\sqrt{3}b-1}{4}$×b×cosC,
化简可得:cosC=$\frac{4b(\sqrt{3}-\sqrt{3}{b}^{2}+6b)}{8b({b}^{2}-2\sqrt{3}b-1)}$,
解得:cosC=-$\frac{\sqrt{3}}{2}$,
故答案为:-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查余弦定理的应用,不等式解法的应用,根据三角函数的值求角,判断最大边为c,是解题的关键,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
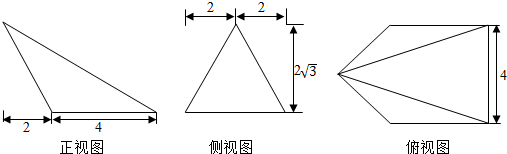
| A. | 48π | B. | 52π | C. | $\frac{172}{3}$π | D. | $\frac{196}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com