Question

16．已知关于x的一元二次方程x²+2mx+2m+1=0有两个根，求满足下列条件的m的取值范围．
（1）两个根都小于0；
（2）其中一个根在区间（-1，0）内，另一个根在区间（1，2）内．

Answer 1

分析 （1）抛物线f（x）=x²+2mx+2m+1与x轴的两个交点都在区间（-∞，0）中，列出不等式组，求解即可．
（2）抛物线 f（x）=x²+2mx+2m+1与x轴的交点分别在区间（-1，0）和 （1，2）内，列出不等式组求解即可．

解答 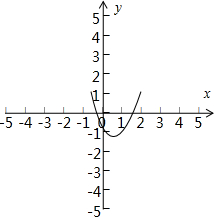解：（1）由题意知，抛物线f（x）=x²+2mx+2m+1与x轴的两个交点都在区间（-∞，0）中，
即$\left\{\begin{array}{l}△=4{m^2}-4（{2m+1}）≥0\\-m＜0\\ f（0）＞0\end{array}\right.$解得：$m≥1+\sqrt{2}$．
（2）由题意知，抛物线 f（x）=x²+2mx+2m+1与x轴的交点分别在区间（-1，0）和 （1，2）内，
画出示意图，如图，
得  $\left\{\begin{array}{l}f（0）=2m+1＜0\\ f（{-1}）=2＞0\\ f（1）=4m+2＜0\\ f（2）=6m+5＞0\end{array}\right.⇒\left\{\begin{array}{l}m＜-\frac{1}{2}\\ m∈R\\ m＜-\frac{1}{2}\\ m＞-\frac{5}{6}\end{array}\right.$，
则$-\frac{5}{6}＜m＜-\frac{1}{2}$．

点评 本题考查二次函数的性质的应用，函数的零点，考查转化思想以及数形结合思想的应用．