
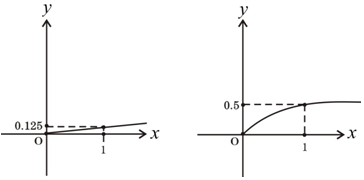
分析 (1)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;
(2)由(1)的结论,我们设设投资债券类产品x万元,则股票类投资为20-x万元.这时可以构造出一个关于收益y的函数,然后利用求函数最大值的方法进行求解.
解答 解:(1)f(x)=k1x,g(x)=${k}_{2}\sqrt{x}$,
f(1)=$\frac{1}{8}$=k1,g(1)=k2=$\frac{1}{2}$,
∴f(x)=$\frac{1}{8}$x(x≥0),g(x)=$\frac{1}{2}\sqrt{x}$(x≥0)
(2)设:投资债券类产品x万元,则股票类投资为20-x万元.
y=f(x)+g(20-x)=$\frac{x}{8}+\frac{1}{2}\sqrt{20-x}$(0≤x≤20)
令t=$\sqrt{20-x}$,则y=$\frac{20-{t}^{2}}{8}+\frac{1}{2}t$=-$\frac{1}{8}(t-2)^{2}+3$.
所以当t=2,即x=16万元时,收益最大,ymax=3万元.
点评 函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
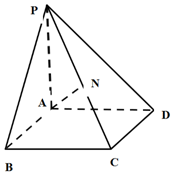 如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点.
如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x2 | B. | y=x-1 | C. | y=x${\;}^{\frac{1}{2}}$ | D. | y=x3-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{11}{8}$ | D. | $-\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com