
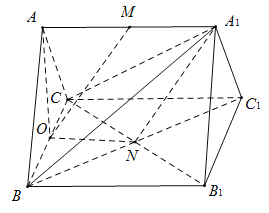
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
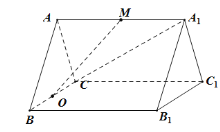
(1)求证:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 为
为![]() 的中点,可得
的中点,可得![]() ,结合
,结合![]() ,得到四边形
,得到四边形![]() 为平行四边形,则
为平行四边形,则![]() ,再由线面平行的判定定理,可得
,再由线面平行的判定定理,可得![]() 平面
平面![]() ;
;
(2)由![]() 平面
平面![]() ,点
,点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,利用线面垂直的判定和性质求得
的距离,利用线面垂直的判定和性质求得![]() ,从而可求出
,从而可求出![]() 和
和![]() ,利用等积法得
,利用等积法得![]() ,化简计算可求得点
,化简计算可求得点![]() 到平面
到平面![]() 的距离,从而得出点
的距离,从而得出点![]() 到平面
到平面![]() 的距离,即可得出结果.
的距离,即可得出结果.
解:(1)如图,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() 为
为![]() 的中点,
的中点,
又∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
又∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:∵![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
∵三棱柱![]() 为直三棱柱,
为直三棱柱,
则![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
又![]()
![]() ,
,![]() ,
,
则![]() ,
,
![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
连接![]() 和
和![]() ,则
,则![]() ,
,
∵![]() ,
,
而![]() 到底面的距离等于
到底面的距离等于![]() 到底面的距离为
到底面的距离为![]() ,
,
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
而![]() 为
为![]() 的中点,则
的中点,则![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
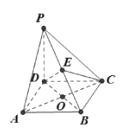
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证: ![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节,一场突如其来的新型冠状病毒感染的肺炎疫情,牵动着我们每个人的心,严重扰乱了大家的正常生活,在全国人民的共同努力下,疫情得到了有效的控制.已知某市A,B,C三个小区的志愿者人数分别为60,40,20,现采用分层抽样的方法从这120名志愿者中随机抽取6人去支援夕阳红敬老院.若再从这6人中随机抽取2名作为负责人,则这2名志愿者来自不同小区的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在实数H,使得对任意的
,若存在实数H,使得对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“和有界数列”.下列说法正确的是( )
为“和有界数列”.下列说法正确的是( )
A.若![]() 是等差数列,且公差
是等差数列,且公差![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
B.若![]() 是等差数列,且
是等差数列,且![]() 是“和有界数列”,则公差
是“和有界数列”,则公差![]()
C.若![]() 是等比数列,且公比
是等比数列,且公比![]() ,则
,则![]() 是“和有界数列”
是“和有界数列”
D.若![]() 是等比数列,且
是等比数列,且![]() 是“和有界数列”,则
是“和有界数列”,则![]() 的公比
的公比![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求f(x)的最大值;
(2)设函数![]() ,若对任意实数
,若对任意实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求a的取值范围;
,求a的取值范围;
(3)若数列![]() 的各项均为正数,
的各项均为正数,![]() ,
,![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)

(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com