
【题目】已知正四棱锥![]() 的底面边长为
的底面边长为![]() ,侧棱
,侧棱![]() ,E为侧棱PB上一点且
,E为侧棱PB上一点且![]() ,在
,在![]() 内(包括边界)任意取一点F,则
内(包括边界)任意取一点F,则![]() 的取值范围为__________.
的取值范围为__________.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】某疾病有甲、乙两种类型,对甲型患者的有效治疗只能通过注射药物Y,而乙型患者可以服药物A进行有效治疗,对该疾病患者可以通过药物A的临床检验确定甲型或乙型.检验的方法是:如果患者利用药物A完成第一个疗程有效,就可以确定是乙型;否则进行第二个疗程,如果完成第二个疗程有效,也可以确定是乙型,否则确定是甲型.为了掌握这种疾病患者中甲型、乙型所占比例,随机抽取100名患者作为样本通过药物A进行临床检验,检验结果是:样本中完成第二个疗程有效的患者是完成第一个疗程有效的患者的60%,且最终确定为甲型患者的有36人.
(1)根据检验结果,将频率视作概率,在利用药物A完成第一个疗程无效的患者中仼选3人,求其中甲型患者恰为2人的概率;
(2)该疾病的患者通过治疗,使血浆中某物质t的浓度降低到![]() 或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:
或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:![]() )的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数
)的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数![]() 和每个疗程后样本血浆中t的平均浓度
和每个疗程后样本血浆中t的平均浓度![]() 的数据作了初步处理,得到下面的散点图及一些统计量的值.
的数据作了初步处理,得到下面的散点图及一些统计量的值.
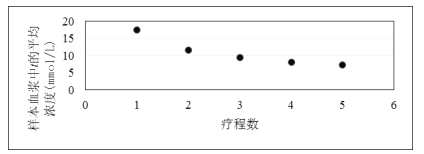
|
|
|
|
|
|
|
3 | 11.0 | 0.46 | 262.5 | 30.1 | 55 | 1.458 |
/span>
上表中![]() ,
,![]() .
.
①根据散点图直接判断(不必说明理由),![]() 与
与![]() 哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
②患者在享受基本医疗保险及政府专项补助后,自己需承担的费用z(单位:元)与x,y的关系为![]() .在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
.在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为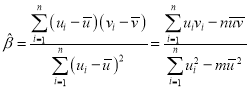 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作两条相互垂直的直线
分别作两条相互垂直的直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 的交点为
的交点为![]() ,三角形
,三角形![]() 面积的最大值为1.
面积的最大值为1.
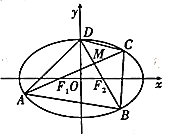
(1)求椭圆![]() 的方程;
的方程;
(2)当四边形![]() 的面积
的面积![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.

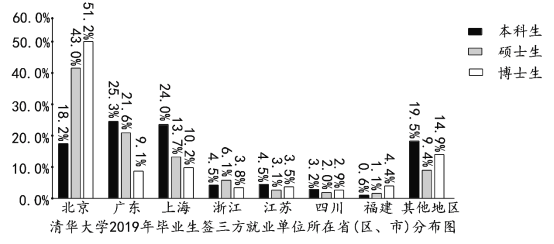
则下列选项错误的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】精准扶贫点用2400元的资金为贫困户购买良种羊羔,共有肉用山羊、毛用绵羊、产奶山羊三种羊羔,价格均为每只300元,若要求每种羊羔至少买1只,则所有可能的购买方案总数为( )
A.12B.14C.21D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直线![]() 与
与![]() 相交于
相交于![]() 两点,且满足:①
两点,且满足:①![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2;②直线
为坐标原点)的斜率之和为2;②直线![]() 与圆
与圆![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com