（2014•湖北模拟）实数ai（i=1，2，3，4，5，6）满足（a2﹣a1）2+（a3﹣a2）2+（a4﹣a3）2+（a5﹣a4）2+（a6﹣a5）2=1则（a5+a6）﹣（a1+a4）的最大值为（ ）
A.3 B.2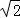
C.
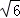D.1
B
【解析】
试题分析：由柯西不等式可得：[（a2﹣a1）2+（a3﹣a2）2+（a4﹣a3）2+（a5﹣a4）2+（a6﹣a5）2]（1+1+1+4+1）≥[（a2﹣a1）+（a3﹣a2）+（a4﹣a3）+2（a5﹣a4）+（a6﹣a5）]2，结合条件，即可得出结论．
【解析】
由柯西不等式可得：
[（a2﹣a1）2+（a3﹣a2）2+（a4﹣a3）2+（a5﹣a4）2+（a6﹣a5）2]（1+1+1+4+1）
≥[（a2﹣a1）+（a3﹣a2）+（a4﹣a3）+2（a5﹣a4）+（a6﹣a5）]2=[（a5+a6）﹣（a1+a4）]2，
∴[（a5+a6）﹣（a1+a4）]2≤8，
∴（a5+a6）﹣（a1+a4）≤2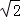
，
∴（a5+a6）﹣（a1+a4）的最大值为2，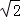
故选B．
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：解答题
已知数列{an}的各项都是正数，且满足：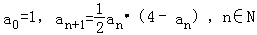
．
（1）求a1，a2；
（2）证明an＜an+1＜2，n∈N．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷（解析版） 题型：填空题
（2014•辽宁）对于c＞0，当非零实数a，b满足4a2﹣2ab+b2﹣c=0且使|2a+b|最大时，
+
+
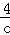的最小值为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：填空题
（2014•长安区三模）己知x，y∈（0，+∞），若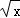
+3
＜k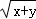
恒成立，利用柯西不等式可求得实数k的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题
已知a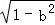
+b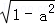
=1，则以下成立的是（ ）
A.a2+b2＞1 B.a2+b2=1 C.a2+b2＜1 D.a2b2=1
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题
反证法证明三角形的内角中至少有一个不小于60°，反设正确的是（ ）
A.假设三内角都不大于60° B.假设三内角都小于60°
C.假设三内角至多有一个大于60° D.假设三内角至多有两个小于60°
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题
用反证法证明“方程ax2+bx+c=0（a≠0）至多有两个解”的假设中，正确的是（ ）
A.至多有一个解 B.有且只有两个解
C.至少有三个解 D.至少有两个解
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：选择题
“执果索因”是下列哪种证明方法的特点（ ）
A.数学归纳法 B.反证法 C.分析法 D.综合法
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题
（2014•吉安二模）已知f（x）=|x﹣1|+|x+m|（m∈R），g（x）=2x﹣1，若m＞﹣1，x∈[﹣m，1]，不等式f（x）＜g（x）恒成立，则实数m的取值范围是（ ）
A.（﹣1，﹣
] B.（﹣1，﹣） C.（﹣∞，﹣] D.（﹣1，+∞）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com