
| A. | 2 | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{3}-1}}{2}$ |
分析 由正弦函数的性质,分段求得函数的值域,结合m≤f(x)≤n得到m,n的范围,从而可求出n-m的最小值.
解答 解:函数f(x)=sinx在x∈[-$\frac{7π}{6}$,$-\frac{π}{2}$]上为减函数,在[$-\frac{π}{2}$,-$\frac{π}{3}$]上为增函数,
∴当x∈[-$\frac{7π}{6}$,$-\frac{π}{2}$]时,f(x)∈[-1,$\frac{1}{2}$];当x∈[$-\frac{π}{2}$,-$\frac{π}{3}$]时,f(x)∈[-1,$-\frac{\sqrt{3}}{2}$].
∴当x∈[-$\frac{7π}{6}$,-$\frac{π}{3}$]时,函数的值域为[-1,$\frac{1}{2}$].
∵当x∈[-$\frac{7π}{6}$,-$\frac{π}{3}$]时,m≤f(x)≤n恒成立,
∴m≤-1,n≥$\frac{1}{2}$.
则n-m的最小值是$\frac{1}{2}-(-1)=\frac{3}{2}$.
故选:C.
点评 本题考查了三角函数的最值,考查了正弦函数的性质,是基础题.


科目:高中数学 来源: 题型:选择题
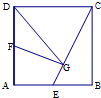 如图所示,正方形ABCD的边长为2,E,F分别为AB,AD的中点,G为线段CE上的一个动点,设$\frac{CG}{CE}$=x,S△GDF=y,则函数y=f(x)的图象大致是( )
如图所示,正方形ABCD的边长为2,E,F分别为AB,AD的中点,G为线段CE上的一个动点,设$\frac{CG}{CE}$=x,S△GDF=y,则函数y=f(x)的图象大致是( )| A. | 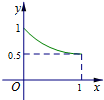 | B. | 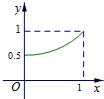 | C. | 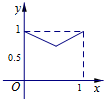 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A. | O-ABC是正三棱锥(底面为正三角形,顶点在底面的投影为底面的中心) | |
| B. | 直线OB∥平面ACD | |
| C. | OD⊥平面ABC | |
| D. | 直线CD与平面ABC所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{26}^{2}$103C${\;}_{5}^{2}$ | B. | A${\;}_{26}^{2}$A${\;}_{10}^{3}$ | ||
| C. | (C${\;}_{26}^{1}$)2A${\;}_{10}^{3}$C${\;}_{5}^{2}$ | D. | A${\;}_{26}^{2}$103 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
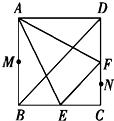 在边长为4cm的正方形ABCD中,E,F分别为BC,CD的中点,M,N分别为AB,CF的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,重合后的点记为B,构成一个三棱锥,则MN与平面AEF的位置关系是MN∥平面AEF.
在边长为4cm的正方形ABCD中,E,F分别为BC,CD的中点,M,N分别为AB,CF的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,重合后的点记为B,构成一个三棱锥,则MN与平面AEF的位置关系是MN∥平面AEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com