
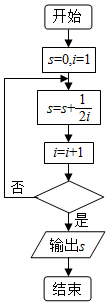
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )| A. | i>5 | B. | i<5 | C. | i>6 | D. | i<6 |
分析 由本程序的功能是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值,由S=S+$\frac{1}{2i}$,故我们知道最后一次进行循环时的条件为i=5,当i>5应退出循环输出S的值,由此不难得到判断框中的条件.
解答 解:∵S=$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$,
并由流程图中S=S+$\frac{1}{2i}$,故循环的初值为1,终值为5,步长为1,
故经过5次循环才能算出S=$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值,
故i≤5,应不满足条件,继续循环,
∴应i>5,应满足条件,退出循环,
填入“i>5”.
故选:A.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
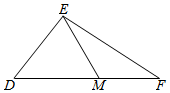 如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.
如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
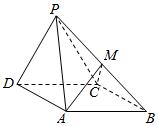 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,面PCD⊥面ABCD,PC=PD=CD=2,点M为线段PB上异于P、B的点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,面PCD⊥面ABCD,PC=PD=CD=2,点M为线段PB上异于P、B的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
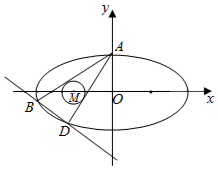 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点为A(0,1),离心率为$\frac{{\sqrt{3}}}{2}$.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点为A(0,1),离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,3) | C. | (-5,4) | D. | (0,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com