
【题目】已知函数f(x)=lnx﹣ ![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(3)若f(x)>x2在(1,+∞)上恒成立,求a的取值范围.
【答案】
(1)解:∵f(x)=lnx﹣ ![]() ,
,
∴f(x)的定义域为(0,+∞), ![]() ,
,
∵a>0,∴f′(x)>0,
∴f(x)在(0,+∞)上单调递增
(2)解:由(1),当a≥0时,f(x)在[1,e]上单调递增,
∴f(x)min=f(1)=﹣a= ![]() ,
,
∴a=﹣ ![]() ,不舍题意,舍;
,不舍题意,舍;
当﹣e<a<0时,f(x)在[1,﹣a]上单调递减,在[﹣a,e]上单调递增,
∴f(x)min=f(﹣a)=ln(﹣a)+1= ![]() ,解得a=﹣
,解得a=﹣ ![]() ;
;
当a<﹣e时,f(x)在[1,e]上单调递增,
∴f(x)min=f(1)=﹣a= ![]() ,解得a=﹣
,解得a=﹣ ![]() ,不合题意,舍;
,不合题意,舍;
综上所述,a=﹣ ![]()
(3)解:∵ ![]() ,∴a>xlnx﹣x3,
,∴a>xlnx﹣x3,
令g(x)=xlnx﹣x3,则g′(x)=lnx+1﹣3x2, ![]() ,
,
当x>1时,g'(x)<0,∴g′(x)在(1,+∞)上单调递减,
∴g′(x)<g′(1)=2<0,
∴g(x)在(1,+∞)上单调递减,
∴g(x)<g(1)=﹣1.
∴a≥﹣1.
∴f(x)>x2在(1,+∞)上恒成立,a的取值范围是[﹣1,+∞)
【解析】(1)f(x)的定义域为(0,+∞), ![]() ,由此利用导数性质能求出f(x)在(0,+∞)上单调递增.(2)由(1)根据a的取值范围分类讨论,由此利用导数性质能求出a的值.(3)由
,由此利用导数性质能求出f(x)在(0,+∞)上单调递增.(2)由(1)根据a的取值范围分类讨论,由此利用导数性质能求出a的值.(3)由 ![]() ,得a>xlnx﹣x3 , 令g(x)=xlnx﹣x3 , 由此利用导数性质能求出a的取值范围.
,得a>xlnx﹣x3 , 令g(x)=xlnx﹣x3 , 由此利用导数性质能求出a的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 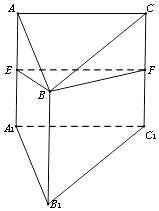
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,下顶点为
,下顶点为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且三角形
,且三角形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相切,过焦点
相切,过焦点![]() ,
, ![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学.从这7名成员中随机抽4人参加高中示范校验收活动问卷调查.
(Ⅰ)设![]() 为事件“选出的4人中既有文科生又有理科生”,求事件
为事件“选出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)设![]() 为选出的4人中男生人数与女生人数差的绝对值,求随机变量
为选出的4人中男生人数与女生人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
参照独立性检验附表,得到的正确结论是( )
A.有99%的把握认为“选择过马路的方式与性别有关”
B.有99%的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,且2acosA=ccosB+bcosC.
(1)求cosA及a的值;
(2)若b2+c2=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 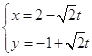 (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求曲线 ![]() 的普通方程与曲线
的普通方程与曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)试判断曲线 ![]() 与
与 ![]() 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com