
【题目】如图,△ABC为正三角形,且BC=CD=2,CD⊥BC,将△ABC沿BC翻折.
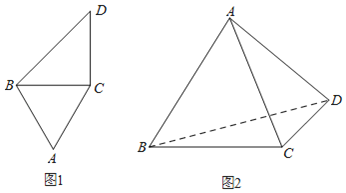
(1)当AD=2时,求证:平面ABD⊥平面BCD;
(2)若点A的射影在△BCD内,且直线AB与平面ACD所成角为60°,求AD的长.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)根据长度关系得到AE⊥平面BCD,得到证明.
(2)取BC中点O,BD中点E,连接AO,OE,得HQ⊥平面ACD,计算HQ![]() ,AH
,AH![]() ,计算得到答案.
,计算得到答案.
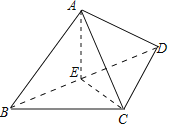
(1)若AD=2,又AB=AC=2,则A在底面BCD内的射影为△BCD的外心,
∵△BCD为直角三角形,且∠BCD=90°,
∴A在底面BCD内的射影E落在BD的中点上,
∴AE⊥平面BCD,而AE平面ABD,
∴平面ABD⊥平面BCD;
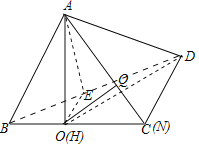
(2)取BC中点O,BD中点E,连接AO,OE,
可得BC⊥平面AOE,过A作AH⊥OE于H,过H作HN∥BC交CD于N,
连接AN,作HQ⊥AN于Q,得HQ⊥平面ACD,
点B到平面ACD的距离为2HQ,则sin60![]() ,得HQ
,得HQ![]() ,
,
设AH=x,有![]() ,解得x
,解得x![]() ,即AH
,即AH![]() ,
,
又AO![]() ,∴H与O重合,
,∴H与O重合,
则AD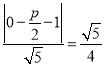 .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若![]() 为真命题,则
为真命题,则![]() ,
,![]() 均为假命题;
均为假命题;
B.命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若“
,若“![]() ”则“
”则“![]() ”的否命题为真命题;
”的否命题为真命题;
D.“平面向量![]() 与
与![]() 的夹角为钝角”的充要条件是“
的夹角为钝角”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,过点P(-2,2)的直线l与抛物线C交于A,B两点.
(1)当点P为A、B的中点时,求直线AB的方程;
(2)求|AF||BF|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,且a≠1.命题P:函数f(x)=logax在(0,+∞)上为增函数;命题Q:函数g(x)=x2﹣2ax+4有零点.
(1)若命题P,Q满足P真Q假,求实数a的取值范围;
(2)命题S:函数y=f(g(x))在区间[2,+∞)上值恒为正数.若命题S为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知S的身高约为
,已知S的身高约为![]() 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按![]() 米处理)
米处理)
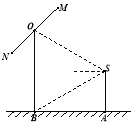
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1左右焦点为F1,F2直线(
1左右焦点为F1,F2直线(![]() 1)x
1)x![]() y
y![]() 0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
(1)求椭圆C的方程;
(2)设P为椭圆C上任一点,过焦点F1,F2的弦分别为PM,PN,设![]() λ1
λ1![]() λ2
λ2![]() ,求λ1+λ2的值.
,求λ1+λ2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(卷号)2040818101747712
(题号)2050752239689728
(题文)
在平面直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知直线![]() 的参数方程为
的参数方程为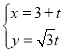 (
(![]() 为参数),曲线C的极坐标方程为
为参数),曲线C的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.
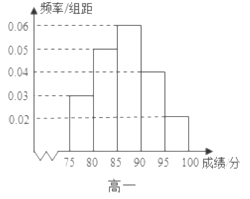
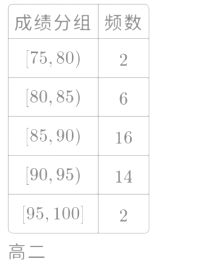
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一、高二两个年级知识竞赛的平均分分别为![]() ,试估计
,试估计![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com