
分析 (Ⅰ)求出|$\overrightarrow{a}$$+\overrightarrow{b}$|的表达式,结合x的范围,从而求出|$\overrightarrow{a}$$+\overrightarrow{b}$|的范围即可;
(Ⅱ)先求出$\overrightarrow{a}$•$\overrightarrow{b}$,再求出|$\overrightarrow{a}$-$\overrightarrow{b}$|,从而求出f(x)的表达式,进而求出其最小值及x的取值.
解答 解:(Ⅰ)|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(cos\frac{3x}{2}+cos\frac{x}{2})}^{2}{+(sin\frac{3x}{2}-sin\frac{x}{2})}^{2}}$=$\sqrt{2+2cos2x}$
因为x∈[$\frac{π}{2}$,$\frac{3π}{2}$],π≤2x≤3π,
所以:-1≤cos2x≤1,
∴0≤|$\overrightarrow{a}$+$\overrightarrow{b}$|≤2;
(Ⅱ)∵$\overrightarrow{a}$•$\overrightarrow{b}$=cos$\frac{3x}{2}$cos$\frac{x}{2}$-sin$\frac{3x}{2}$sin$\frac{x}{2}$=cos2x,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2-2cos2x}$,
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-|$\overrightarrow{a}$-$\overrightarrow{b}$|=cos2x-2|sinx|,
x∈[$\frac{π}{2}$,π]时,
f(x)=1-2sin2x-2|sinx|=1-2sin2x-2sinx,
此时0≤sinx≤1,令t=sinx,则t∈[0,1],
∴f(t)=1-2t2-2t=-2${(t+\frac{1}{2})}^{2}$+$\frac{3}{2}$,
当t=1时,f(t)最小,f(t)的最小值是-3,
此时,sinx=1,x=$\frac{π}{2}$,
同理可求x∈[π,$\frac{3π}{2}$]时,f(x)的最小值是-3,
此时,sinx=-1,x=$\frac{3π}{2}$.
点评 本题考查了平面向量数量积的运算,考查函数的最值问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$i | D. | $\frac{1}{4}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )
已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )| A. | 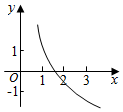 | B. | 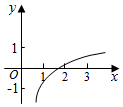 | C. |  | D. | 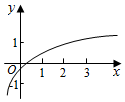 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-4y2=2 | B. | x2-y2=2 | C. | x2-2y2=1 | D. | 2x2-y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线a,b都平行于同一个平面 | B. | 直线a平行于直线b所在的平面 | ||
| C. | 直线a,b都垂直于同一条直线 | D. | 直线a,b都垂直于同一个平面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com